電動機運転時データから関係諸量を求める問題。
- 難易度 ★★★★★
- 重要度 ★★★★☆

運転時の出力を求める
同期電動機1相分の等価回路は以下のように表される。
同様の問題が出た際は、最初にこの図を作図してから始めることを推奨する。
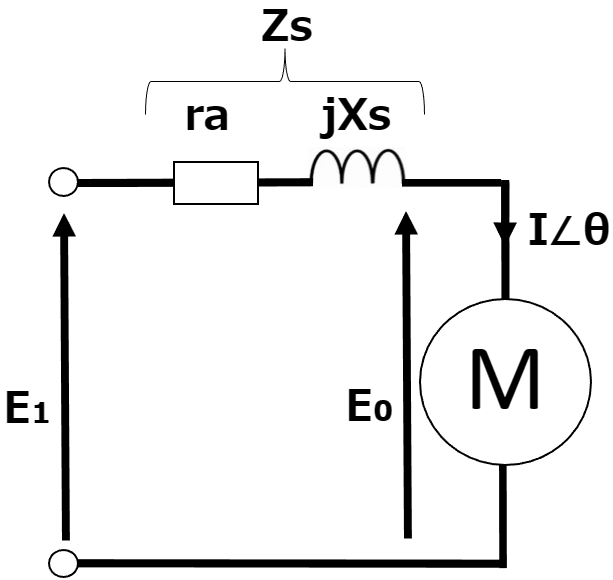
M:負荷、E₀:誘導起電力[V]、E₁:端子電圧[V]※相電圧、I∠θ:電機子電流[A]※E₁とより位相がθ°遅れ、ra:電機子抵抗[Ω]、jXs:同期リアクタンス[Ω]、Zs:同期インピーダンス[Ω]
電動機の出力の公式
\begin{eqnarray}
Po&=& \sqrt{3}IVcosθη \\
\end{eqnarray}
Po:電動機の出力[kW]、I:電流[A]、V:端子電圧[V]、cosθ:力率、η:効率
計算に必要な諸量は問題文にあるので、公式にあてはめ計算する。
\begin{eqnarray}
Po&=& \sqrt{3}IVcosθη \\
&=& \sqrt{3}\times{96}\times{6300}\times{1.0}\times{0.956} \\
&=&{1001.423}\times{10^3}{[kW]} \\
\end{eqnarray}
よって問Aの答えは1.00×10³[kW]であることが分かる。
3相分の損失を求める
効率は以下の考え方である。
\begin{eqnarray}
η=\frac{出力}{入力}&=& \frac{出力}{出力+損失} \\
\end{eqnarray}
1)の出力は効率ηをかけているので、全ての損失分が引かれた値である。
この問題は、損失がない状態(=入力)から損失を引けばいいので、まず入力を求める。
\begin{eqnarray}
Po&=& \sqrt{3}IVcosθ \\
&=& \sqrt{3}\times{96}\times{6300}\times{1.0} \\
&=&{1047.513}\times{10^3}{[kW]} \\
\end{eqnarray}
問題文より、エネルギー収支を以下のとおり表すことできる。
\begin{eqnarray}
{入力}&=& {機械損}+{鉄損}+{励磁回路損}+{漂遊負荷損}+{電機子回路損}+{出力} \\
{電機子回路損}&=& {入力}-{機械損}-{鉄損}-{励磁回路損}-{漂遊負荷損}-{出力} \\
Pa&=& {1047.513}-{11}-{9}-{6}-{4}-{1001.423} \\
&=& {16.09 ≒ 16.1[kW]} \\
\end{eqnarray}
よって問Bの答えは16.1[kW]であることが分かる。
1相分の電機子抵抗を求める
また、電機子回路損は電機子で発生する電力損失であるから、
\begin{eqnarray}
Pa&=& 3I^2ra \\
ra&=& \frac{Pa}{3I^2} \\
&=& \frac{16.09\times{10^3}}{3\times{96^2}} \\
&=& 0.5819 ≒ 5.82\times{10^{-1}}{[Ω]} \\
\end{eqnarray}
よって問Cの答えは5.82×10³[Ω]であることが分かる。
1相分の誘導起電力を求める
既に述べたとおり、同期機の等価回路は以下の図で表される。
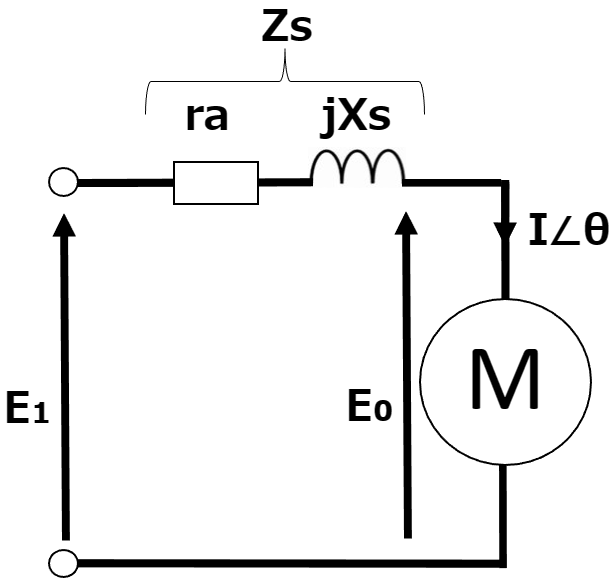
この回路はよく以下のようなベクトル図で表される。この図もよく出題されている。
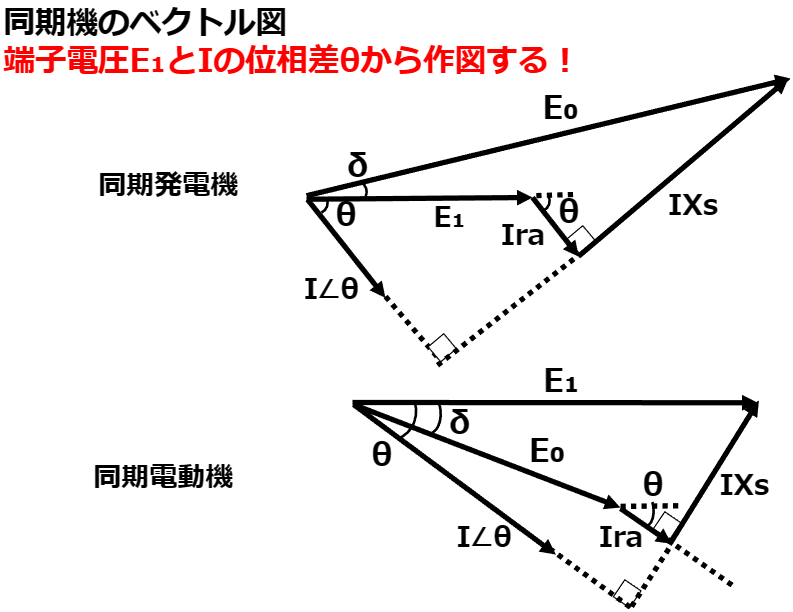
δ:負荷角
まず、等価回路を作図する。以下のようになる。
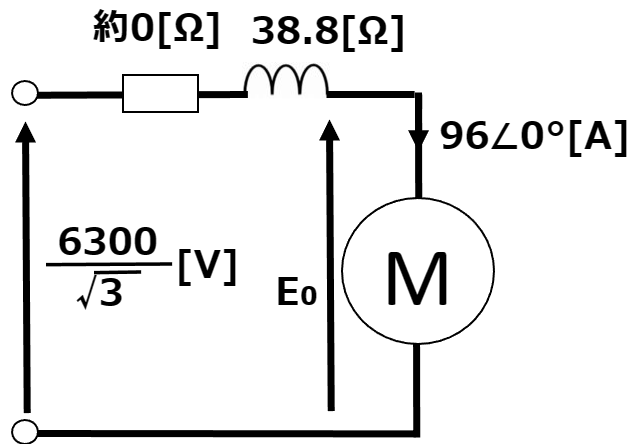
一般に、E₁に対してIはθ°の位相差を持っているが、問題文より力率が1.0である。
cosθが1となるとき、三角関数からθ=0°である。
よって、IとE₁は同じ位相(ベクトルが平行)と判断できる。
IとIraは同じ位相差であるから、Iraの位相も同様にE₁と同じである。
IXsはIraと90°位相差があるので、今回はE₁と90°位相差となる。
これらを踏まえると、ベクトル図は以下のとおりになる。
※問題文よりraの影響を無視できるのでIraは無視できるが、一応作図している。
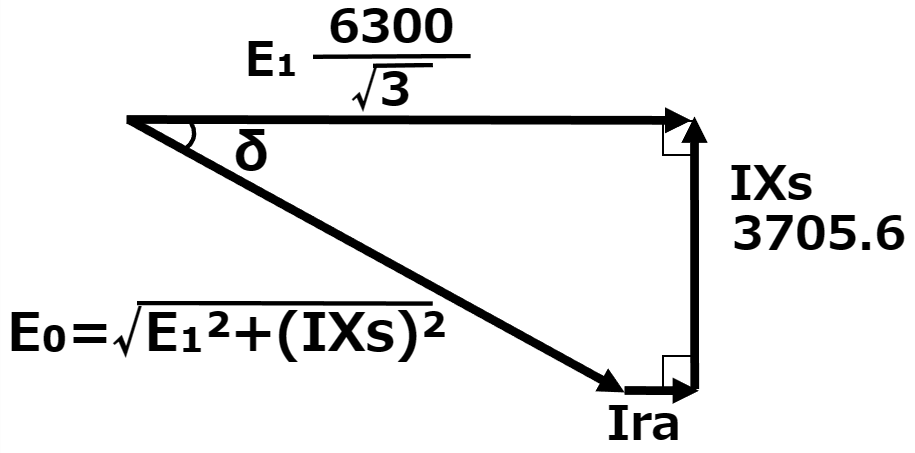
ベクトル図より、誘導起電力E₀はE₁とIXsからなる直角三角形の斜辺であるから、以下のようになる。
\begin{eqnarray}
E0&=& \sqrt{(\frac{E₁}{\sqrt3})^2+{(IXs)^2}} \\
&=& \sqrt{(\frac{6300}{\sqrt3})^2+{3705.6^2}} \\
&=& {5192.44 ≒ 5.19[kV]} \\
\end{eqnarray}
よって問Dの答えは5.19[kV]であることが分かる。



コメント