配電線路の力率改善時の変化量を求める問題。
- 難易度 ★★★★☆
- 重要度 ★★★★☆
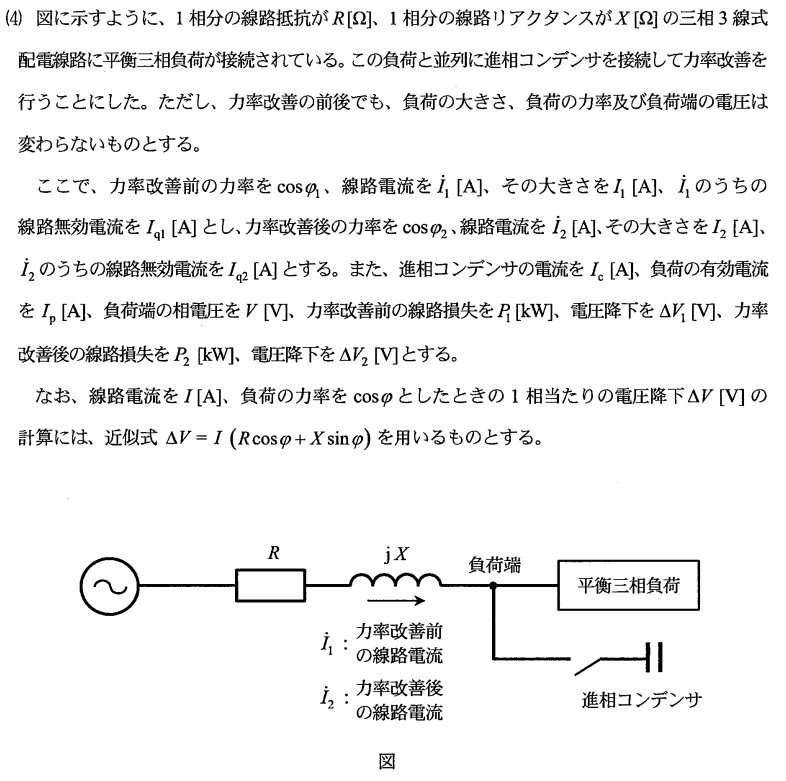

1相あたりの線路損失を求める
回路の電圧や抵抗は一定であるから、変化するのは電流である。(解答群からもわかる)
また、問題文から力率改善前の電流はİ₁、改善後の電流İ₂である。あとは各式を整理するだけでよい。
\begin{eqnarray}
P₁-P₂&=& {I₁^2}{r}-{I₂^2}{r} \\
&=& {(I₁^2-I₂^2)}{r} \\
\end{eqnarray}
よって問9の答えはエであることが分かる。
1相あたりの電圧降下を求める
\begin{eqnarray}
ΔV&=& I(Rcosθ+Xsinθ) \\
\end{eqnarray}
ΔV:電圧降下[V]、I:電流[A]、R:回路抵抗[Ω]、X:リアクタンス[Ω]、cosθ:力率、sinθ:無効率
抵抗成分とリアクタンス成分はそれぞれcosθとsinθをかけることで算出できる。
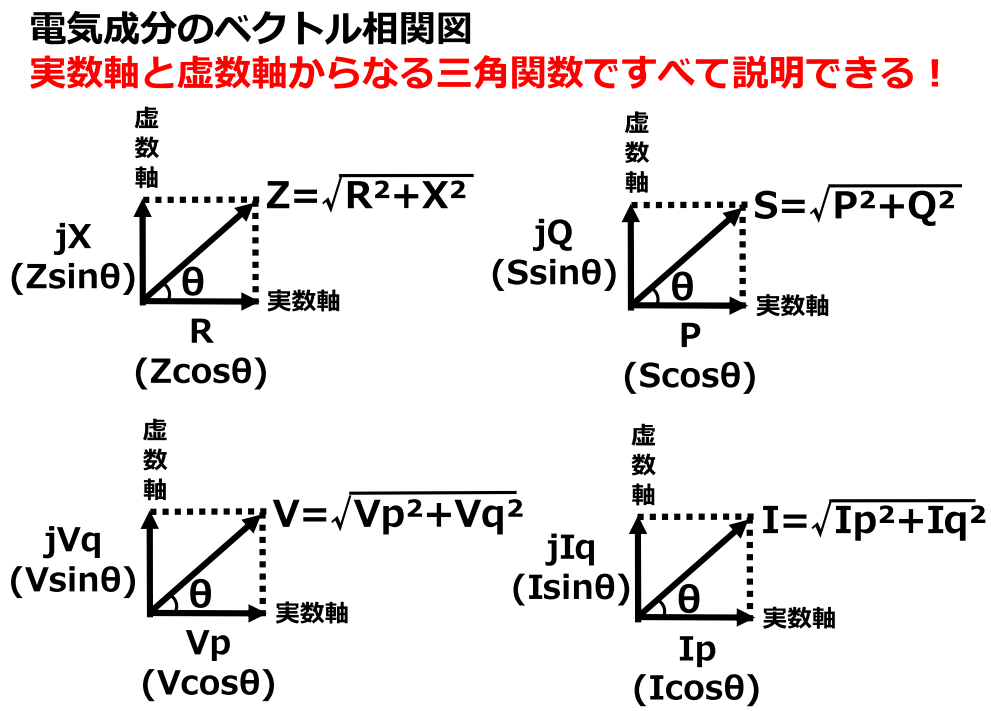
公式に代入しΔVを導いていく。
\begin{eqnarray}
ΔV₁-ΔV₂&=& I₁(Rcosθ₁+Xsinθ₁)-I₂(Rcosθ₂+Xsinθ₂) \\
&=& I₁Rcosθ₁+I₁Xsinθ₁-I₂Rcosθ₂-I₂Xsinθ₂ \\
\end{eqnarray}
ここで、I₁Rcosθ₁に着目し分解すると、以下のようになる。
\begin{eqnarray}
I₁&=& \frac{P₁}{\sqrt{3}Vcosθ₁} \\
I₁Rcosθ₁&=& \frac{P₁}{\sqrt{3}Vcosθ₁}\times{Rcosθ₁} \\
\end{eqnarray}
つまり、cosθが変化しても打ち消すことができるので、I₁cosθ₁を考慮する必要がなくなる。
同様にRも一定であるから、この項は力率改善前後で打ち消すことができる。
また、IsinθはIqであるから、
\begin{eqnarray}
ΔV₁-ΔV₂&=& I₁Rcosθ₁+I₁Xsinθ₁-I₂Rcosθ₂-I₂Xsinθ₂ \\
&=& I₁Xsinθ₁-I₂Xsinθ₂ \\
&=& Iq₁X-Iq₂X \\
&=& (Iq₁-Iq₂)X \\
\end{eqnarray}
よって問10の答えはウであることが分かる。
力率改善後の線路損失を求める
1)で公式はP=I²Rを用いることが分かっており、2)でIはcosθのみの影響で変化することを利用した。
問題文にはいくつかの数値が与えられているが、上記よりcosθの比で求めることができる。
\begin{eqnarray}
P₁&=& {I₁^2}{r} \\
&=& (\frac{P₁}{\sqrt{3}Vcosθ₁})^2\times{R} \\
\end{eqnarray}
ここで、cosθ以外の値は不変であるからP₁はcosθ²のみで変化することが分かる。
\begin{eqnarray}
P₁:P₂&=& \frac{1}{cosθ₁^2}{:}\frac{1}{cosθ₂^2} \\
830:P₂&=& \frac{1}{0.85^2}{:}\frac{1}{0.95^2} \\
\frac{P₂}{0.85^2}&=& \frac{830}{0.95^2} \\
P₂&=&{664.45[W]} \\
\end{eqnarray}
\begin{eqnarray}
P₁-P₂&=&{830}-{664.45}\\
&=& {165.55} ≒ {166[W]} \\
\end{eqnarray}
よって問Aの答えは166[W]であることが分かる。
力率改善後の1相あたりの電圧降下を求める
2)の問題より使用する公式が分かっているので、公式にあてはめる。
\begin{eqnarray}
ΔV₁&=& {Iq₁}{X} \\
&=& {(I₁sinθ₁)}{X} \\
&=& (\frac{P₁}{\sqrt{3}Vcosθ₁})\times{sinθ₁X} \\
\end{eqnarray}
ここで、改善前後で一定の項と変化する項で分けると、以下のようになる。
\begin{eqnarray}
ΔV₁&=& (\frac{P₁X}{\sqrt{3}V})\times\frac{sinθ₁}{cosθ₁} \\
\end{eqnarray}
このことから、sinθとcosθの比でΔVが求まることが分かる。
よって先にsinθ₁とsinθ₂を求める。
\begin{eqnarray}
sinθ₁&=& \sqrt{1-cosθ₁^2} \\
&=&\sqrt{1-0.85^2} \\
&=& {0.5268} \\
sinθ₂&=& \sqrt{1-cosθ₂^2} \\
&=&\sqrt{1-0.95^2} \\
&=& {0.3122} \\
\end{eqnarray}
必要な項を求めることができたので、sinθとcosθの比からΔV₂を求める。
\begin{eqnarray}
ΔV₁:ΔV₂&=& \frac{sinθ₁}{cosθ₁}{:}\frac{sinθ₂}{cosθ₂} \\
10:ΔV₂&=& \frac{0.52678}{0.85}{:}\frac{0.3122}{0.95} \\
&=& {0.6197}{:}{0.3286} \\
0.6197ΔV₂&=& {3.286} \\
ΔV₂&=& {5.3025[V]} \\
\end{eqnarray}
\begin{eqnarray}
ΔV₁-ΔV₂&=& {10}-{5.3025} \\
&=& {4.6975} ≒ {4.7[V]}\\
\end{eqnarray}
よって問Dの答えは4.7[V]であることが分かる。



コメント