工場配電の知識を問う問題です。過去問にも類題が多いので確実に解けるようにしましょう。
- 難易度 ★★★☆☆
- 重要度 ★★★★★
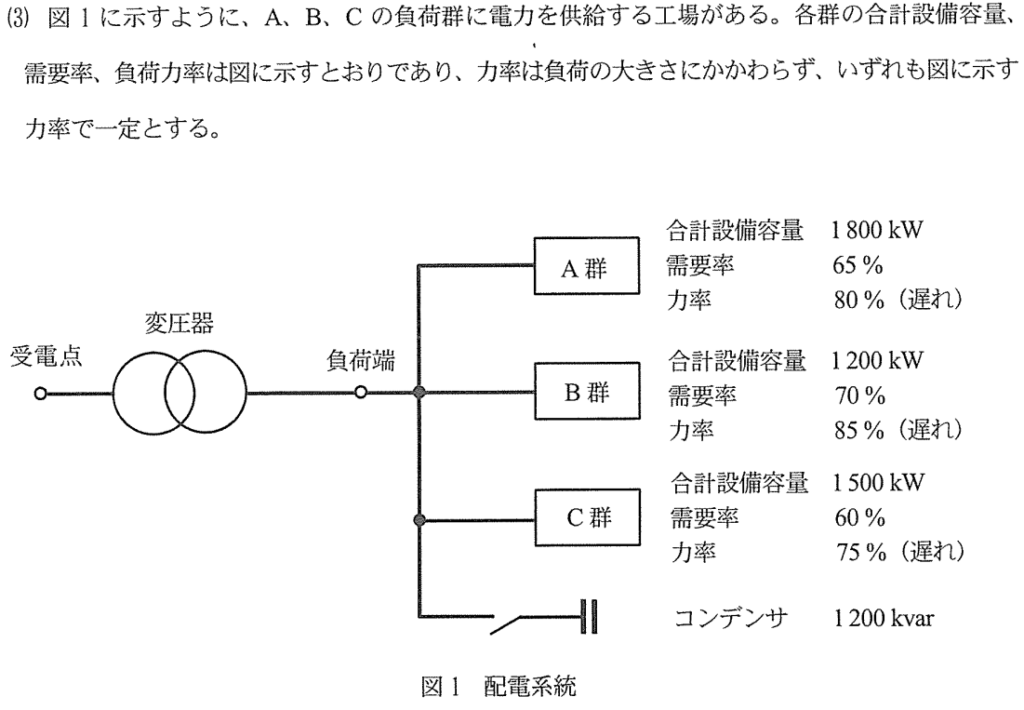

最大需要電力、最大無効電力を求める
ポイント
\begin{eqnarray}
負荷率&=& \frac{平均電力[kw]}{最大電力[kw]} \\
需要率&=& \frac{最大電力[kw]}{設備容量[kw]}\\
\end{eqnarray}
ポイントの式から最大需要電力Pa[kW]を求める。
\begin{eqnarray}
需要率&=& \frac{最大電力[kw]}{設備容量[kw]}\\
最大電力&=& {需要率}\times{設備容量} \\
Pa&=& {0.65}\times{1800} \\
&=& {1170}[kW] \\
\end{eqnarray}
よって問8の解答はウ となることがわかる。
有効電力P、皮相電力S、無効電力Qの関係から問9の解答、最大無効電力Qa[kVar]を求める。
\begin{eqnarray}
Sa&=& \frac{Pa}{cosθa}\\
&=& \frac{1170}{0.8} \\
Qa&=& {Sa}\times{sinθa} \\
&=& \frac{1170}{0.8}\times{0.6} \\
&=& {877.5} ≒ 878[kVar] \\
\end{eqnarray}
よって問9の解答はアとなることが分かる。
不等率を求める
ポイント
$$不等率=\frac{各負荷の最大需要電力の和[kw]}{合成最大需要電力[kw]}$$
※不等率は必ず1以上となる
問題文より、合成最大需要電力[kw]が与えられているので
\begin{eqnarray}
合成最大需要電力[kw]&=& {1000}+{600}+{750}\\
&=& {2350}[kW] \\
\end{eqnarray}
各負荷の電力最大需要電力の和[kw]を求める。1)と同様にB群、C群の最大需要電力Pb、最大無効電力Qcを求められるので
\begin{eqnarray}
Pb&=& {0.7}\times{1200}\\
&=& {840}[kW] \\
\end{eqnarray}
\begin{eqnarray}
Pc&=& {0.6}\times{1500} \\
&=&{900}[kW] \\
\end{eqnarray}
\begin{eqnarray}
各負荷の最大需要電力の和[kw]&=& {1170}+{840}+{900} \\
&=& {2910}[kW] \\
\end{eqnarray}
\begin{eqnarray}
不等率&=& \frac{各負荷の最大需要電力の和[kw]}{合成最大需要電力[kw]} \\
&=& \frac{2910}{2350} \\
&=& {1.2382} ≒ 1.24 \\
\end{eqnarray}
よって問Aの解答は1.24となることが分かる。
力率を求める
コンデンサ接続後の力率をを求めるためには改善前の無効電力の合計を算出する必要がある。
問題図より各負荷の力率が違うので、まずは各負荷の無効率を求める。
\begin{eqnarray}
sin^2θ+cos^2θ&=& {1}\\
sinθb&=& \sqrt{1-cos^2θb}\\
&=& \sqrt{1-0.85^2}\\
&=& {0.5267}\\
\end{eqnarray}
\begin{eqnarray}
sinθc&=& \sqrt{1-cos^2θc}\\
&=& \sqrt{1-0.75^2}\\
&=& {0.6614}\\
\end{eqnarray}
求めた無効率を用いて各負荷の無効電力を求め、改善前の無効電力の合成を求める。
\begin{eqnarray}
Qa&=& {Sa}\times{sinθa}\\
&=& \frac{1000}{0.8}\times{0.6}\\
&=& {750}[kVar]\\
\end{eqnarray}
\begin{eqnarray}
Qb&=& {Sb}\times{sinθb}\\
&=& \frac{600}{0.85}\times{0.5267}\\
&=& {371.78}[kVar]\\
\end{eqnarray}
\begin{eqnarray}
Qc&=& {Sc}\times{sinθc}\\
&=& \frac{750}{0.75}\times{0.6614}\\
&=& {661.4}[kVar]\\
\end{eqnarray}
\begin{eqnarray}
改善前無効電力の合計[kVar]&=& {750}+{371.78}+{661.4}\\
&=& {1783.18}[kW]\\
\end{eqnarray}
問題文より、1200[kVar]のコンデンサを接続したことで無効電力が改善するので
\begin{eqnarray}
改善後無効電力[kVar]&=& {1783.18}-{1200}\\
&=& {583.18}[kVar]\\
\end{eqnarray}
有効電力P、皮相電力S、無効電力Qの関係から 皮相電力S[kVA]を求める。
\begin{eqnarray}
S&=& \sqrt{P^2+Q^2}\\
&=&\sqrt{2350^2+583.18^2}\\
&=& {2421.28}[kVA]\\
\end{eqnarray}
問題2)より、合成最大需要電力P[kW]が分かっているので
\begin{eqnarray}
cosθ&=& \frac{有効電力P[kW]}{皮相電力S[kVA]}\\
&=&\frac{2350}{2421.28}\\
&=& {0.9706} ≒ 97.1[%]\\
\end{eqnarray}
よって問Bの解答は97.1となることが分かる。



コメント