日負荷曲線を用いた配電コントロールの問題です。過去問にも類題が多いので確実に解けるようにしましょう。
- 難易度 ★★☆☆☆
- 重要度 ★★★★★

負荷率を求める
\begin{eqnarray}
負荷率&=& \frac{平均電力[kw]}{最大電力[kw]} \\
需要率&=& \frac{最大電力[kw]}{設備容量[kw]}\\
\end{eqnarray}
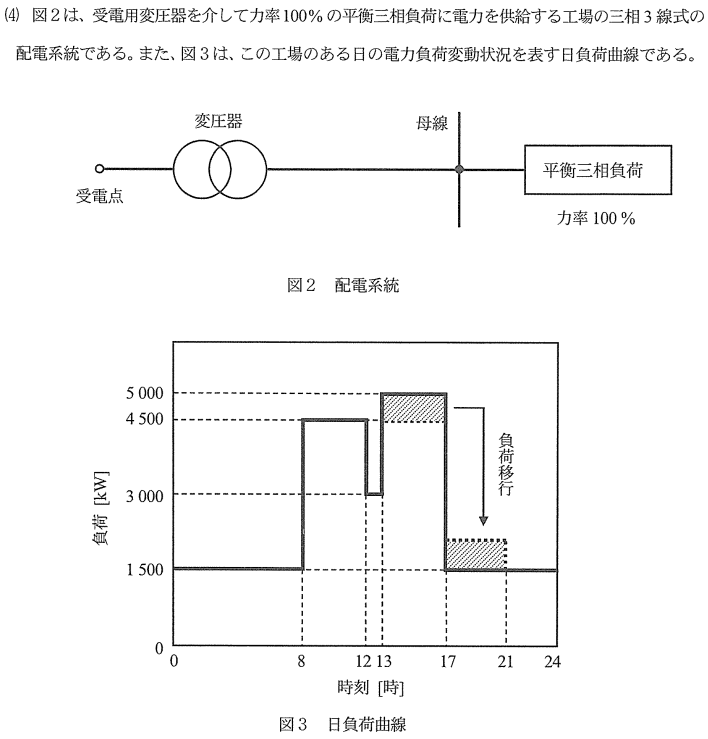
問題文より最大電力[kW]が分かっているため、平均電力 [kW] が分かれば負荷率[%]を求めることができる。まずは図3から平均電力 [kW] を求める。
\begin{eqnarray}
1日の平均電力[kW]&=& \frac{1日の負荷電力の合計[kw]}{24時間} \\
&=& \frac{1500\times15+4500\times4+5000\times4+3000\times1}{24}\\
&=& {2645.833[kw]}\\
\end{eqnarray}
平均電力が分かったので、公式に代入し負荷率を求める。
\begin{eqnarray}
負荷率&=& \frac{平均電力[kw]}{最大電力[kw]} \\
&=& \frac{2645.833}{4500}\\
&=& {0.58796 ≒ 58.8[%]}\\
\end{eqnarray}
よって問Cの答えは58.8であることが分かる。
損失電力量を求める
\begin{eqnarray}
Pc&=& {α}^2\times{Pcn}\times{T} \\
&=&(\frac{P}{Pn})^2\times{Pcn}\times{T}\\
\end{eqnarray}
Pc:変圧器の銅損[kw]、α:負荷率、Pcn:全負荷(定格負荷)時の銅損[kw]、
T:運転時間[h]、P:実負荷[kw]、Pn:定格負荷[kw]
※P、PnはそれぞれS、Snでも計算できる。
負荷移行前の損失電力量を求めるため、図3から各負荷時の損失電力量を算出し、合計する。
※損失電力量=銅損+鉄損であるが、鉄損は負荷変動の影響を受けないため無視できる。
※問題文より力率は常に100%であるので、変圧器定格[kVA]は×1をすることで[kw]に変換できる。
\begin{eqnarray}
Pc5000&=& (\frac{5000}{{7500}\times{1}})^2\times{58}\times{4} \\
&=&{103.111[kwh]}\\
\end{eqnarray}
\begin{eqnarray}
Pc1500&=& (\frac{1500}{{7500}\times{1}})^2\times{58}\times{15} \\
&=&{34.8[kwh]}\\
\end{eqnarray}
\begin{eqnarray}
Pc3000&=& (\frac{3000}{{7500}\times{1}})^2\times{58}\times{1} \\
&=&{9.28[kwh]}\\
\end{eqnarray}
\begin{eqnarray}
Pc4500&=& (\frac{4500}{{7500}\times{1}})^2\times{58}\times{4} \\
&=&{83.52[kwh]}\\
\end{eqnarray}
\begin{eqnarray}
Pc&=& 103.111+34.8+9.28+83.52 \\
&=&{230.711[kwh]}\\
\end{eqnarray}
続いて負荷移行後の電力量を求める。
\begin{eqnarray}
Pc1500&=& (\frac{1500}{{7500}\times{1}})^2\times{58}\times{11} \\
&=&{25.52[kwh]}\\
\end{eqnarray}
\begin{eqnarray}
Pc4500&=& (\frac{4500}{{7500}\times{1}})^2\times{58}\times{8} \\
&=&{167.04[kwh]}\\
\end{eqnarray}
\begin{eqnarray}
Pc3000&=& (\frac{3000}{{7500}\times{1}})^2\times{58}\times{1} \\
&=&{9.28[kwh]}{※} \\
\end{eqnarray}
※3000kWで運転する時間は移行前と同じなので計算結果を流用してOK
\begin{eqnarray}
Pc2000&=& (\frac{2000}{{7500}\times{1}})^2\times{58}\times{4} \\
&=&{16.497[kwh]}\\
\end{eqnarray}
\begin{eqnarray}
Pc’&=& 25.52+167.04+9.28+16.497 \\
&=&{218.337[kwh]}\\
\end{eqnarray}
負荷移行前と移行後の損失電力量が分かったので、差を求める。
\begin{eqnarray}
Pc’&=& 230.711-218.337 \\
&=&{12.374[kwh]}\\
\end{eqnarray}
よって問Dの答えは12.4であることが分かる。



コメント