工場配電の知識を問う問題。特に2)の公式問題は確実に解けるようにしたい。
- 難易度 ★★★☆☆
- 重要度 ★★★★★



問題と解答群を俯瞰する
(1)の問題全体と解答群全体を眺めた時、以下の点に気付きたい。
- ア~ウ、オは配電線路用語である。問1もしくは問2の選択肢となる。
- ケとコは長さの話である。問3の選択肢となる。
- カ~クは変圧器用語である。問4の選択肢となる。

工場における電力損失の問題
配電線路の電力損失は、一般に以下の公式で求めることができる。
\begin{eqnarray}
P&=& 3I^2r[kw]
\end{eqnarray}
P:3相分の線路損失[kW]、I:線路電流[A]、r:線路抵抗[Ω]
式より、線路電流と線路抵抗の2つしか変数がないことが分かる。
問題文に線路電流は与えられているから、線路抵抗であると分かる。
よって問1の解答はオ となることがわかる。
次に、線路電流の低減対策である。線路電流は一般に以下の公式で求めることができる。
\begin{eqnarray}
P&=& \sqrt{3}IVcosθ[kw] \\
I&=& \frac{P}{\sqrt{3}Vcosθ}[A] \\
\end{eqnarray}
P:負荷の有効電力[kW]、I:線路電流[A]、V:端子電圧[V]、cosθ:力率
式より、負荷の有効電力と電圧、力率の3つしか変数がないことが分かる。
力率は分母にあるため、力率が大きいほど線路電流は小さくなる。
力率を改善するのは進相コンデンサである。
よって問2の解答はア となることがわかる。
また、過去問の計算問題では、進相コンデンサと投入して力率改善を行い、電力損失を低減させる問題が頻出している。このことからも進相コンデンサであると分かる。
次に、問題3であるが、1)より線路抵抗を低減する対策であることが分かる。
こう長とは長さのことなので、「抵抗を減らすためには線路の長さをどうすればよいか」を問われている。解答群には長さを指す解答がケとコの2つしかない。
抵抗は一般に以下の式で求めることができる。
\begin{eqnarray}
R&=& ρ\frac{l}{A}[Ω] \\
\end{eqnarray}
R:抵抗[Ω]、ρ抵抗率[Ωm]、l:導体の長さ[m]、A:導体の断面積[㎡]
公式より、抵抗は長さに比例する。
よって問3の解答はコ となることがわかる。
工場における負荷設備の問題
負荷設備の諸係数は、一般に以下の公式で求めることができる。
\begin{eqnarray}
負荷率&=& \frac{平均電力[kw]}{最大電力[kw]} \\
需要率&=& \frac{最大電力[kw]}{設備容量[kw]}\\
\end{eqnarray}
$$不等率=\frac{各負荷の最大需要電力の和[kw]}{合成最大需要電力[kw]}$$
※不等率は必ず1以上となる
公式を問われているだけなので、当てはまる解答を答えるだけである。
この公式は計算でも頻出なので、確実に覚えておきたい。
よって問5~7の解答はオ、エ、キ となることがわかる。
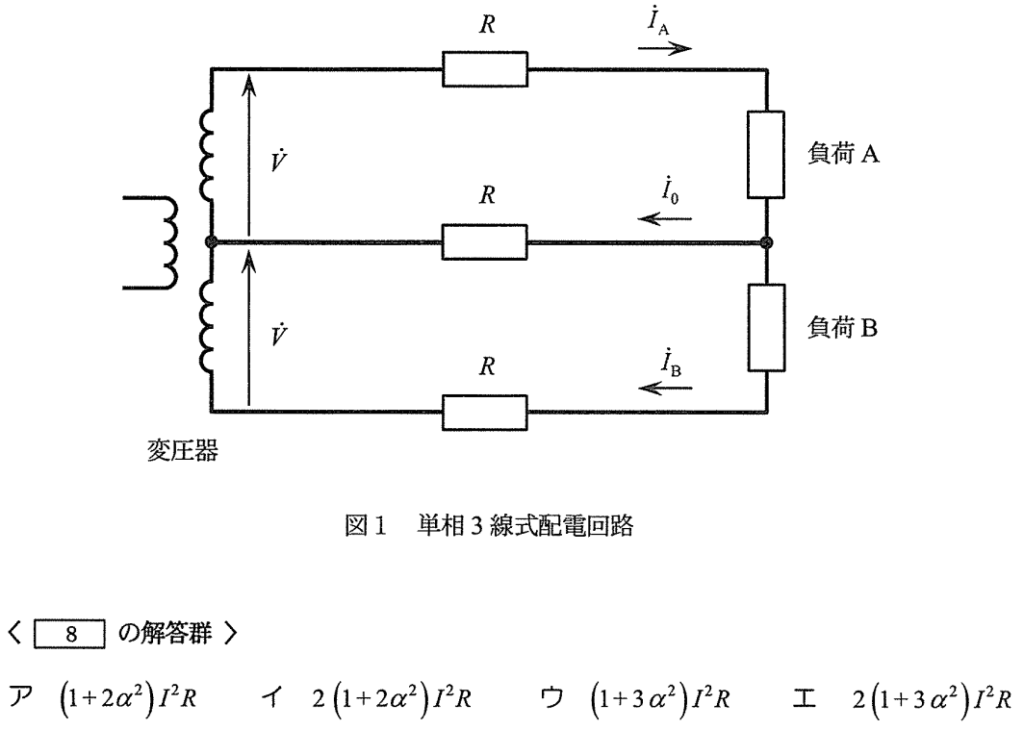
単相3線式配電線路の電力損失の問題
この問題のみ、難易度が高い。各線の電流を文字式で計算する必要があるので、計算ミスをしないよう注意すること。
問題文より、以下の2式が与えられている。
\begin{eqnarray}
Iᴀ+Iʙ&=& 2I\cdots① \\
\end{eqnarray}
\begin{eqnarray}
I₀&=& α(Iᴀ+Iʙ) \\
Iᴀ+Iʙ&=& \frac{I₀}{α}\cdots② \\
\end{eqnarray}
問題文より、最終的にWをIとαを用いることが分かるので、与えられた式からIᴀとIʙの文字を消していく。
①を②に代入すると、
\begin{eqnarray}
2I&=& \frac{I₀}{α} \\
Iα&=& \frac{I₀}{2}\cdots③ \\
\end{eqnarray}
次に、IᴀをIとαを用いて表記するよう変形する。
IᴀとIʙの共通項を持つ式があるので、連立方程式を解く。
\begin{array}{rcccccc}
&I_A+I_B&=&2I \\
+\big{)} &I_A-I_B&=&I_0 \\
\hline
&2I_A&=&2I+I_0 \\
&I_A&=&I+\frac{I_0}{2}\cdots④ \\
\end{array}
④に③を代入すると、
\begin{eqnarray}
I_A&=&I+Iα\cdots⑤ \\
\end{eqnarray}
次に、IʙをIとαを用いて表記するよう変形する。
①の式より、Iᴀは以下のように表せる。
\begin{eqnarray}
Iᴀ+Iʙ&=& 2I\cdots① \\
Iᴀ&=& 2I-Iʙ\cdots⑥ \\
\end{eqnarray}
⑤の式に⑥の式をIᴀ=に変形した式を代入する。
\begin{eqnarray}
I_A&=&I+Iα\cdots⑤ \\
2I-I_B&=&I+Iα \\
-I_B&=&I+Iα-2I \\
&=&-I+Iα \\
I_B&=&I-Iα\cdots⑥ \\
\end{eqnarray}
最後に、IᴀとIʙとI₀から、電力損失Wを求める。③⑤⑦の式を代入する。
\begin{eqnarray}
W&=& I_A^2R+I_B^2R+I_0^2R \\
&=& (I+Iα)^2R+(I-Iα)^2R+(2αI)^2R \\
&=& (I^2+2αI^2+α^2I^2)R+(I^2-2αI^2+α^2I^2)R+4α^2I^2R \\
&=& (1+2α+α^2+1-2α+α^2+4α^2)I^2R \\
&=& (2+6α^2)I^2R \\
&=& 2(1+3α^2)I^2R \\
\end{eqnarray}
よって問8の解答はエとなることが分かる。



コメント