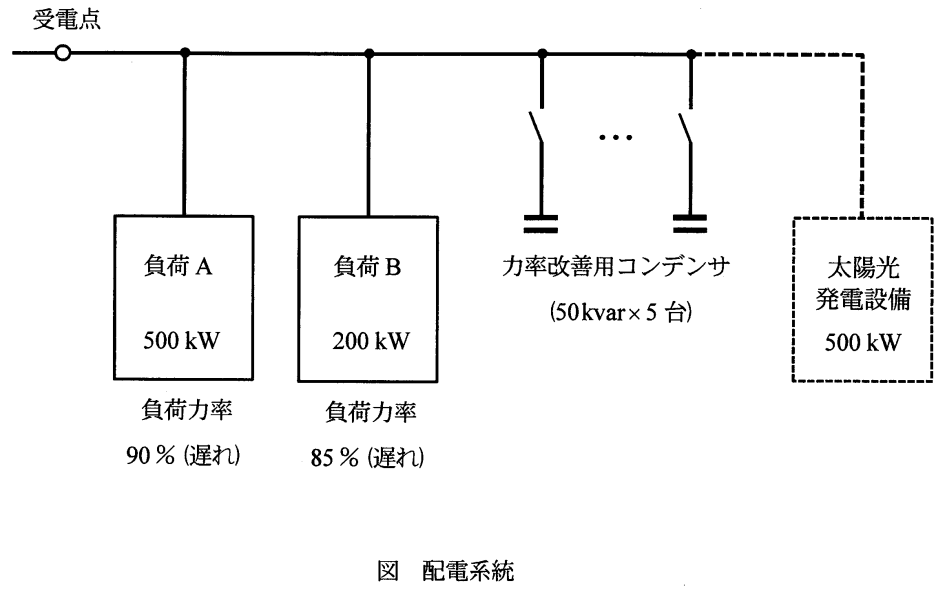
配電線路の力率改善時の変化量を求める問題。ベクトルの考え方を用いる良問であるので、理解しておきたい。
- 難易度 ★★★★☆
- 重要度 ★★★★★


負荷の合成電力を求める
抵抗成分とリアクタンス成分はそれぞれcosθとsinθをかけることで算出できる。
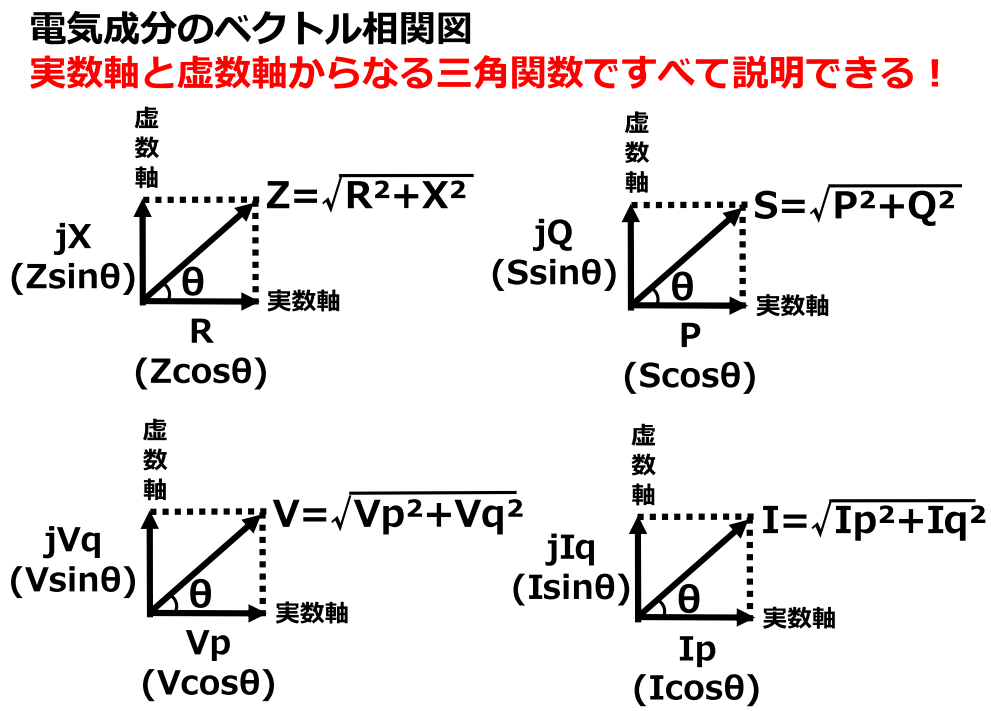
まず、負荷Aと負荷Bの有効電力は500[kW]と200[kW]なので、それらの合計は700[kW]となる。
よって問Aの答えは700[kW]であることが分かる。
次に、無効電力Qを求める必要がある。問題文より、負荷の有効電力Pと力率cosθが与えられているので、これらを用いる。
まず、負荷Aと負荷Bの無効率sinθaとsinθbを求める。
\begin{eqnarray}
sinθa&=& \sqrt{1-cosθa^2} \\
&=&\sqrt{1-0.9^2} \\
&=& {0.4359} \\
\end{eqnarray}
\begin{eqnarray}
sinθb&=& \sqrt{1-cosθb^2} \\
&=&\sqrt{1-0.85^2} \\
&=& {0.5267} \\
\end{eqnarray}
次に、負荷Aと負荷Bの無効電力QaとQbを求め、それらを合計する。
\begin{eqnarray}
Qa&=& {Sa}\times{sinθa}\\
&=& \frac{Pa}{cosθa}\times{sinθa}\\
&=& \frac{500}{0.9}\times{0.4358}\\
&=& {242.111}[kVar]\\
\end{eqnarray}
\begin{eqnarray}
Qb&=& \frac{Pb}{cosθb}\times{sinθb}\\
&=& \frac{200}{0.85}\times{0.5267}\\
&=& {123.929}[kVar]\\
\end{eqnarray}
\begin{eqnarray}
Q&=& Qa+Qb \\
&=& 242.111+123.929 \\
&=& {366.04 ≒ 366}[kVar]\\
\end{eqnarray}
よって問Bの答えは366[kvar]であることが分かる。
コンデンサ投入後の力率を求める
この手の問題が出たときは、以下のベクトル図を思い浮かべると考えやすい。
抵抗成分とリアクタンス成分はそれぞれcosθとsinθをかけることで算出できる。

全体の有効電力と無効電力が700[kW]+j366[kvar]であると分かった。
ここで、コンデンサ(50[kvar])を5台投入するので、投入後の無効電力Q’は以下のようになる。
\begin{eqnarray}
Q’&=& 366-250
&=& {116[kvar]} \\
\end{eqnarray}
ここまでをベクトル図に表すと以下のとおりである。
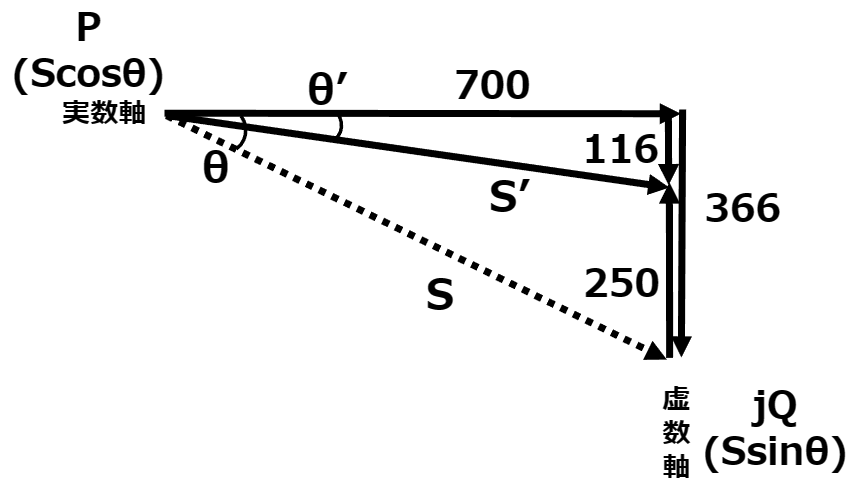
合計ベクトルからS’を求め、総合力率を求めていく。
\begin{eqnarray}
S’&=& \sqrt{P^2+Q’^2} \\
&=& \sqrt{700^2+116^2} \\
&=& \sqrt{490000+13456} \\
&=& 709.546[kVA] \\
\end{eqnarray}
\begin{eqnarray}
cosθ’&=& \frac{P}{S’} \\
&=& \frac{700}{709.546} \\
&=& {0.9865 ≒ 98.7[%]}\\
\end{eqnarray}
よって問Cの答えは98.7[%]であることが分かる。
太陽光発電設備導入後の力率を求める
太陽光発電設備は負荷ではなく発電設備なので、負荷の合計電力は減る方向になる。
導入後のベクトル図は以下のようになる。
ここで、無効電力Qのベクトルは、新たにできる三角形を分かりやすくするため、そのまま横に移動している。
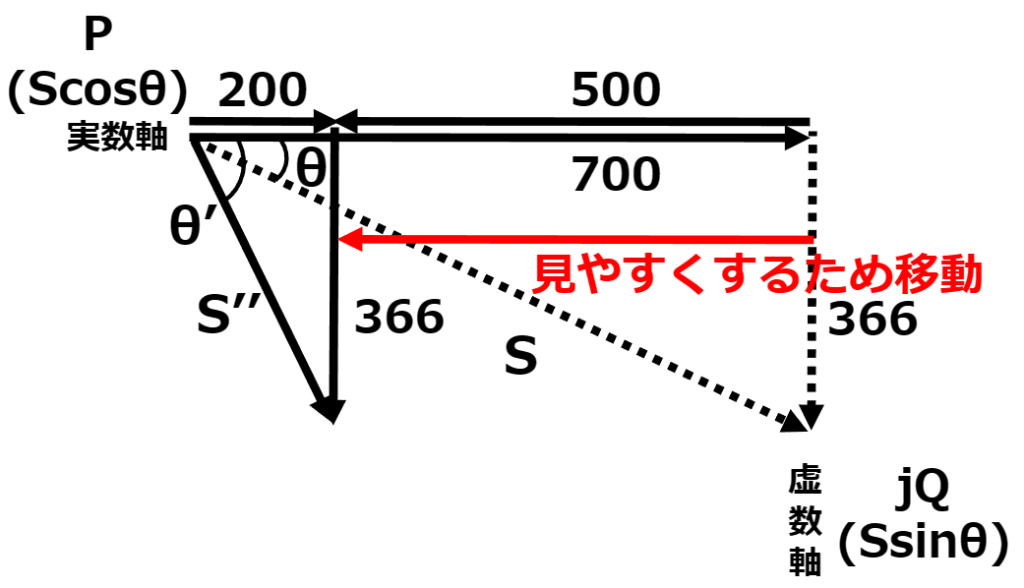
合計ベクトルからS’’を求め、総合力率を求めていく。
\begin{eqnarray}
S’’&=& \sqrt{P^2+Q^2} \\
&=& \sqrt{200^2+366^2} \\
&=& \sqrt{40000+13456} \\
&=& 417.08[kVA] \\
\end{eqnarray}
\begin{eqnarray}
cosθ’&=& \frac{P}{S’} \\
&=& \frac{200}{417.08} \\
&=& {0.4795 ≒ 48.0[%]}\\
\end{eqnarray}
よって問Dの答えは48.0[%]であることが分かる。
目標の力率にするためのコンデンサ投入量を求める
問題をベクトル図に表すと以下のようになる。
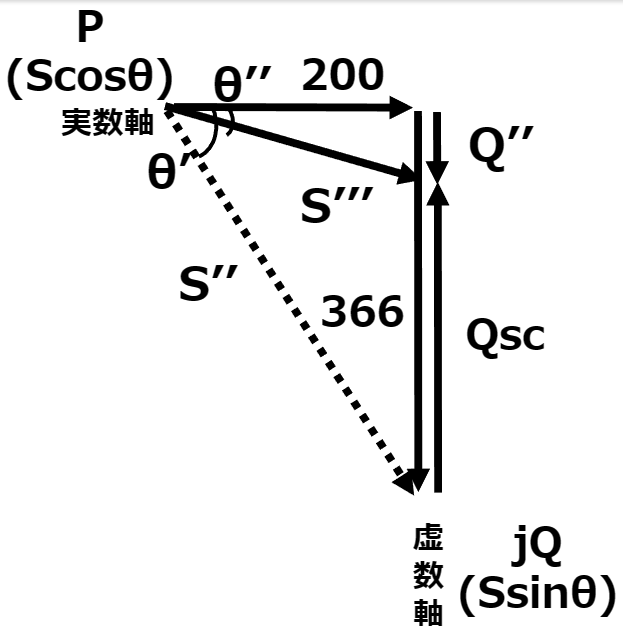
有効電力Pと力率cosθ’’が分かっているので、皮相電力S”を求める。
\begin{eqnarray}
S’’&=& \frac{P}{cosθ’’} \\
&=& \frac{200}{0.98} \\
&=& 204.08[kVA] \\
\end{eqnarray}
有効電力Pと皮相電力S”から、力率改善後の無効電力Q’’を求める。
\begin{eqnarray}
S&=& \sqrt{P^2+Q^2} \\
Q’&=& \sqrt{S’’^2-P^2} \\
&=& \sqrt{204.08^2-200^2} \\
&=& \sqrt{41648.6464-40000} \\
&=& 40.603[kvar] \\
\end{eqnarray}
1)で求めたコンデンサ投入前の無効電力と、今求まった力率改善後の無効電力の差が投入したコンデンサ全容量であるから、コンデンサ全容量は以下のとおりである。
\begin{eqnarray}
Q&=& 366-40.603 \\
&=& 325.397 [kvar] \\
\end{eqnarray}
コンデンサ1個当たり50[kvar]であるから、
\begin{eqnarray}
コンデンサの個数&=& \frac{325.397}{50} \\
&=& 6.507 [個] \\
\end{eqnarray}
よって、6個では目標を達成できないため、問Eの答えは7[個]であることが分かる。
太陽光発電の力率を変更した場合のコンデンサ投入量を求める
問題文より、太陽光発電の出力Pと力率cosθが分かっている。問題文をよく読むと、各値が負荷Aとまったく同じであり、お互いに打ち消すことができる。よって負荷Bのみを考えればよい。
2)で求めた条件は200[kW]、cosθ=98[%]であった。
上述の理由から、3)を負荷B単体で考えると200[kW]、cosθ=98[%]であり、条件は2)と全く同じである。
よって、2)で求めた力率改善後の無効電力Q’’は、3)でも変わらないのでそのまま使うことができる。
また、1)で負荷B単体で発生する無効電力Qbは既に求めている。負荷B自体が変わったわけでもないので、こちらもそのまま使うことができる。
ベクトル図に表すと、以下のようになる。
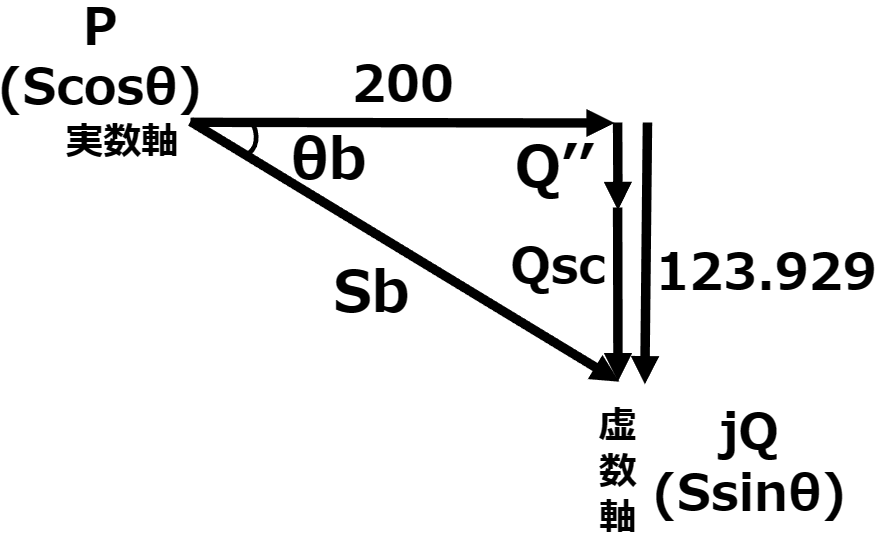
これらを差し引きすると、力率を改善するのに必要なコンデンサ容量Qscが求まる。
\begin{eqnarray}
Qsc&=& Qb-Q’’ \\
&=& 123.929-40.603 \\
&=& {83.326}[kvar]\\
\end{eqnarray}
コンデンサ1個当たり50[kvar]であるから、
\begin{eqnarray}
コンデンサの個数&=& \frac{83.326}{50} \\
&=& 1.666 [個] \\
\end{eqnarray}
よって、1個では目標を達成できないため、問Fの答えは2[個]であることが分かる。



コメント