無負荷試験と短絡試験の結果から、変圧器の損失を求める問題。少し聞きなれない単語もでてくるが、難しい内容ではないので気負わなくてよい。
- 難易度 ★★★☆☆
- 重要度 ★★★★★
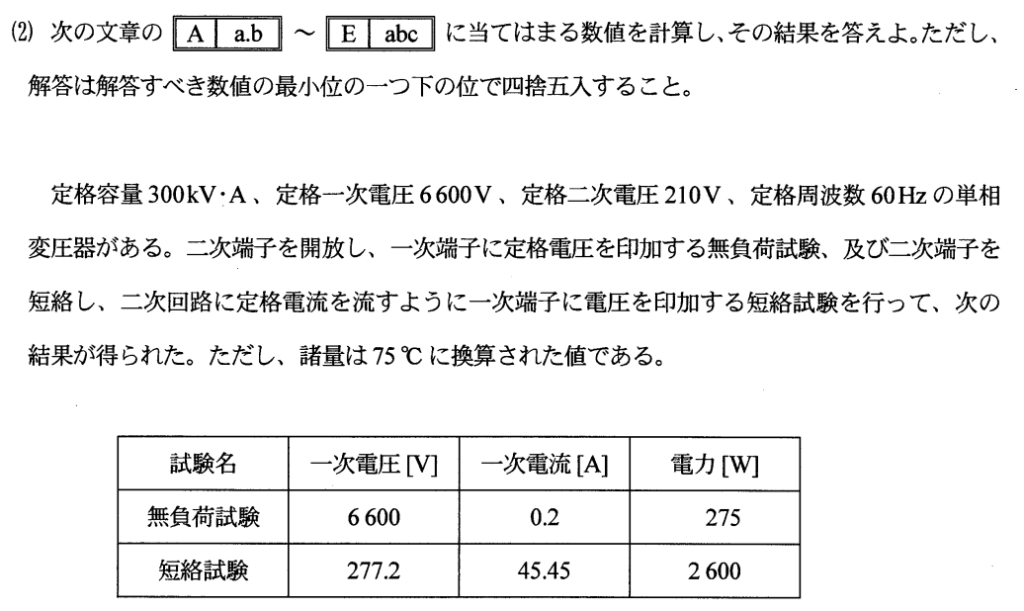

短絡インピーダンスを求める
\begin{eqnarray}
Z&=&\frac{V_1s}{I_1s}
\end{eqnarray}
Z:短絡インピーダンス[Ω]、V₁s:インピーダンス電圧[V](短絡試験時変圧器1次側に定格電流が流れるときの電圧降下)、I₁s:短絡電流[A](短絡試験時は、I₁s=I₁n定格電流となる)
問題文より、短絡試験の結果から求めることができることが分かる。公式に代入すれば求まる。
\begin{eqnarray}
Z&=& \frac{V_1s}{I_1s} \\
&=& \frac{277.2}{45.45} \\
&=& 6.099 ≒ 6.1[Ω] \\
\end{eqnarray}
よって問Aの答えは6.1[Ω]であることが分かる。
基準インピーダンスを求める
基準インピーダンスという単語はあまり出てこないので、慣れない単語に惑わされないこと。要はインピーダンスを求めればよいのである。
問題文より、定格容量300[kVA]の変圧器に6600[V]がかかっている時のインピーダンスZを求める。
インピーダンスを求めるため、この時に流れる電流を求める。この変圧器は単相なので√3は不要である。
\begin{eqnarray}
In&=&\frac{S}{Vn} \\
&=& \frac{300\times10^3}{6600}\\
&=& 45.45[A]\\
\end{eqnarray}
\begin{eqnarray}
Z&=&\frac{Vn}{In} \\
&=& \frac{6600}{45.45}\\
&=& 145.21 ≒ 145.2[Ω]\\
\end{eqnarray}
よって問Bの答えは145.2[Ω]であることが分かる。
パーセント短絡インピーダンスを求める
電圧変動率の近似公式
\begin{eqnarray}
ε&=& \frac{I₂nR₂cosθ+I₂nX₂sinθ}{Vn} \\
&=& pcosθ+qsinθ \\
p&=& \frac{I₂nR₂}{V₂n}\times100 \\
q&=& \frac{I₂nX₂}{V₂n}\times100 \\
%z&=& \sqrt{p^2+q^2} \\
\end{eqnarray}
ε:電圧変動率、I₂n:2次側定格電流[A]、R₂:換算後の1次側、2次側巻線抵抗の合計[Ω]、cosθ:力率、X₂:換算後の1次側、2次側リアクタンスの合計[Ω]、sinθ:無効率、p:百分率抵抗降下[%]、q:百分率リアクタンス降下[%]、V₂n:2次側定格電圧[V]、%z:パーセント短絡インピーダンス[%]
短絡インピーダンスはインピーダンスで発生する電圧降下の割合を指すので、この場合、全体の電圧の中の電圧降下分の割合となる。
前述のとおり、インピーダンス電圧は電圧降下であるから、
\begin{eqnarray}
%z&=&\frac{V_1s}{Vn} \\
&=& \frac{277.2}{6600}\\
&=& 0.042 = 4.20[%]\\
\end{eqnarray}
よって問Cの答えは4.20[%]であることが分かる。
百分率リアクタンス降下を求める
短絡インピーダンス中のリアクタンス成分とは、百分率リアクタンス降下のことである。
電圧変動率の近似公式の以下の部分からも、パーセント短絡インピーダンスが百分率抵抗降下と百分率リアクタンス降下から構成されていることが分かる。
\begin{eqnarray}
p&=& \frac{I₂nR₂}{V₂n}\times100 \\
q&=& \frac{I₂nX₂}{V₂n}\times100 \\
%z&=& \sqrt{p^2+q^2} \\
\end{eqnarray}
パーセント短絡インピーダンスが求まったので、それを用いて百分率リアクタンス降下を求める。
問題文より、抵抗分(百分率抵抗降下)は分かっているので公式に代入する。
\begin{eqnarray}
%z&=& \sqrt{p^2+q^2} \\
q&=& \sqrt{%z^2-p^2} \\
&=& \sqrt{4.20^2-0.867^2} \\
&=& \sqrt{17.64-0.751689} \\
&=& 4.1095 ≒ 4.11[%] \\
\end{eqnarray}
よって問Dの答えは4.11[%]であることが分かる。
エネルギー消費効率を求める
聞きなれないかもしれないが、変圧器のエネルギー消費効率とは、基準負荷率の時の全損失のことを指す。全損失とは無負荷損と負荷損の合計である。
無負荷損は無負荷試験時の電力損失であり、負荷損は短絡試験時の電力損失である。負荷損は負荷率αによって変動するので、
\begin{eqnarray}
P&=& Pi+α^2Pc \\
&=& 275+0.4^2\times2600 \\
&=& 275+416 \\
&=& 691[w] \\
\end{eqnarray}
よって問Eの答えは691[w]であることが分かる。



コメント