日負荷曲線を用いた配電コントロールの問題です。過去問にも類題が多いので確実に解けるようにしましょう。
- 難易度 ★☆☆☆☆
- 重要度 ★★★★★


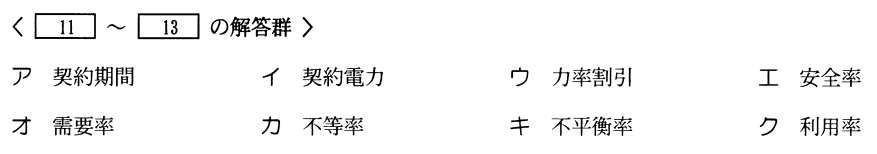
問題文と解答群を俯瞰する
問題全体と解答群全体を眺めた時、以下の点に気付きたい。
- 1)の式はよく使う公式である。問11はオ、問12はカである。
- 問13は電力会社との契約の話である。ア~ウが選択肢となる。
- 1日の中の負荷の量を移動しただけであり、契約の期間には関係がない。
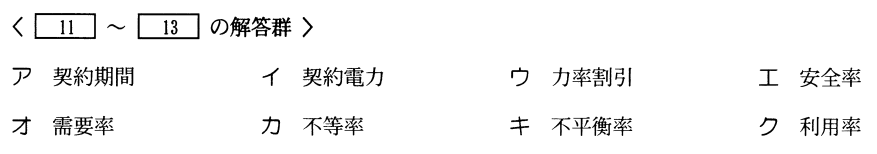
負荷設備の諸係数を考える
この公式は頻出であるので暗記すること。
\begin{eqnarray}
負荷率&=& \frac{平均電力[kw]}{最大電力[kw]} \\
需要率&=& \frac{最大電力[kw]}{設備容量[kw]}\\
\end{eqnarray}
$$不等率=\frac{各負荷の最大需要電力の和[kw]}{合成最大需要電力[kw]}$$
※不等率は必ず1以上となる
よって問11の答えはオ、問12はカであることが分かる。
負荷率を求める
\begin{eqnarray}
負荷率&=& \frac{平均電力[kw]}{最大電力[kw]} \\
需要率&=& \frac{最大電力[kw]}{設備容量[kw]}\\
\end{eqnarray}
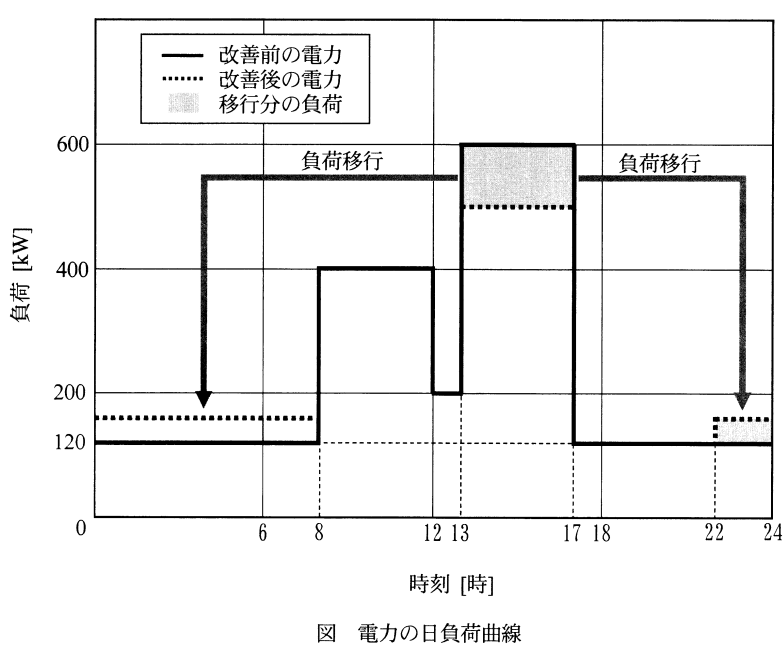
問題文より最大電力[kW]が分かっているため、平均電力 [kW] が分かれば負荷率[%]を求めることができる。まずは図3から平均電力 [kW] を求める。
\begin{eqnarray}
1日の平均電力[kW]&=& \frac{1日の負荷電力の合計[kw]}{24時間} \\
&=& \frac{120\times15+400\times4+200\times1+600\times4}{24}\\
&=& \frac{1800+1600+200+2400}{24}\\
&=& {250[kw]}\\
\end{eqnarray}
平均電力が分かったので、公式に代入し負荷率を求める。
\begin{eqnarray}
負荷率&=& \frac{平均電力[kw]}{最大電力[kw]} \\
&=& \frac{250}{600}\\
&=& {0.41666 ≒ 41.7[%]}\\
\end{eqnarray}
よって問Aの答えは41.7[%]であることが分かる。
負荷率改善に必要な移動電力量を求める
\begin{eqnarray}
負荷率&=& \frac{平均電力[kw]}{最大電力[kw]} \\
最大電力&=& \frac{平均電力[kw]}{負荷率} \\
&=& \frac{250}{0.5} \\
&=& 500[kW] \\
\end{eqnarray}
最大電力が600kWから500kWに下がったため、負荷(図の日負荷曲線の縦軸)の差は100kWである。これが4時間なので、
\begin{eqnarray}
移動させる電力量&=& 100\times4 \\
&=& 400[kWh] \\
\end{eqnarray}
よって問Bの答えは400[kWh]であることが分かる。
電力会社との契約見直し
契約電力がどういうものかわかる場合
契約電力は、最大需要電力で決まる。これが分かれば、すぐにイであると分かる。
契約電力は、大まかにいえば「私たちは最大で●[kW]使うので、余裕を見て電力会社とは▲[kW]の契約としよう」という風に決めるものである。
契約電力がどういうものか分からなかった場合
最初の俯瞰でイ:契約電力、ウ:力率割引のどちらかであることまで絞られている。
力率が悪いと無駄な電力が増える。そのため、高力率で運転している場合は、電力会社から力率割引してもらえる。なお、試験に出たことはないが高力率とは85%を超える力率を指す。
力率cosθは角度θが変わらなければ一定である。θは有効電力Pと無効電力Qからなる角度である。
問題文より、負荷の移動をしたのみであり、コンデンサ投入など力率改善は行っていない。
総消費電力(有効電力)量は変わらないし、無効電力量も変わらないので、角度θは変わらない。よってウではないことが分かる。
これらの考察から、問13の答えはイであることが分かる。



コメント