日負荷曲線を用いた配電コントロールの問題です。過去問にも類題が多いので確実に解けるようにしましょう。
- 難易度 ★★★☆☆
- 重要度 ★★★★★


負荷率を求める
\begin{eqnarray}
負荷率&=& \frac{平均電力[kw]}{最大電力[kw]} \\
需要率&=& \frac{最大電力[kw]}{設備容量[kw]}\\
\end{eqnarray}
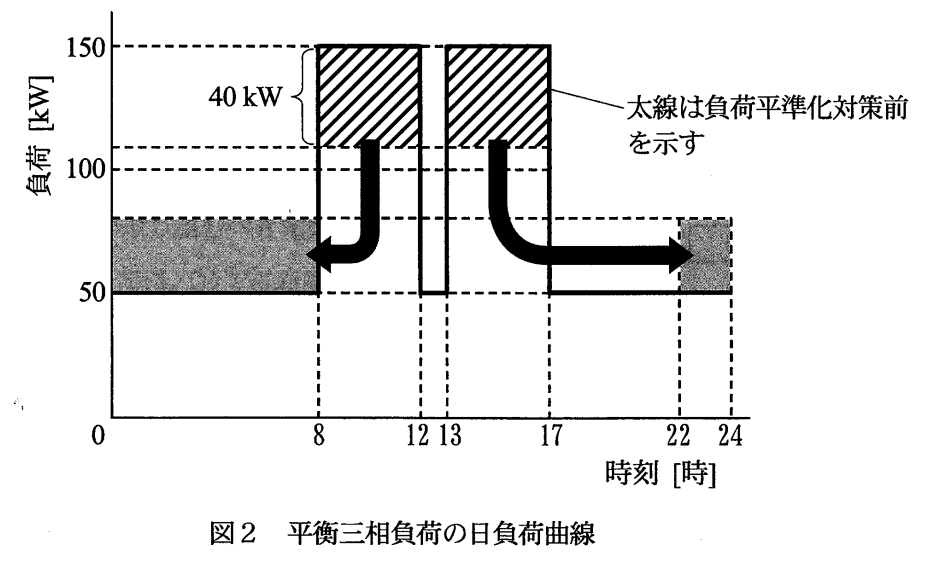
問題文より最大電力が150[kW]から110[kW]になることが分かるため、平均電力 [kW] が分かれば負荷率[%]を求めることができる。まずは図2から平均電力 [kW] を求める。
電力を移動させているが、全体の電力量は移動前後で同じである。移動前の図のほうが計算は楽だろう。
\begin{eqnarray}
1日の平均電力[kW]&=& \frac{1日の負荷電力の合計[kw]}{24時間} \\
&=& \frac{50\times16+150\times8}{24}\\
&=& \frac{800+1200}{24}\\
&=& {83.33[kw]}\\
\end{eqnarray}
平均電力が分かったので、公式に代入し負荷率を求める。
\begin{eqnarray}
負荷率&=& \frac{平均電力[kw]}{最大電力[kw]} \\
&=& \frac{83.33}{110}\\
&=& {0.7575 ≒ 75.6[%]}\\
\end{eqnarray}
よって問Aの答えは75.6[%]であることが分かる。
配電線路に流れる電流を求める
\begin{eqnarray}
P&=& \sqrt{3}IVcosθ \\
\end{eqnarray}
P:有効電力[kW]、I:電流[A]、V:電圧[V]、cosθ:力率
問題文に計算に必要な数値がすべてあるので、公式に代入するだけでよい。
\begin{eqnarray}
I&=& \frac{P}{\sqrt3Vcosθ} \\
&=& \frac{150\times10^3}{\sqrt3\times210\times0.9} \\
&=& {458.2279[A]} \\
\end{eqnarray}
今求まったのは負荷に流れる電流であるので、変圧器2次側の電流にあたる。本問では変圧器1次側の電力損失を出す必要があるので変圧器1次側の電流を求める。
以下は変圧器を考えるうえで必須の公式である。必ず暗記すること。
\begin{eqnarray}
α&=& \frac{N_1}{N_2}=\frac{V_1}{V_2}=\frac{I_2}{I_1} \\
\end{eqnarray}
α:変圧比、N₁:変圧器1次側巻き数、N₂:変圧器2次側巻き数、V₁:変圧器1次側電圧[V]、V₂:変圧器2次側電圧[V]、I₁:変圧器1次側電流[A]、I₂:変圧器2次側電流[A]
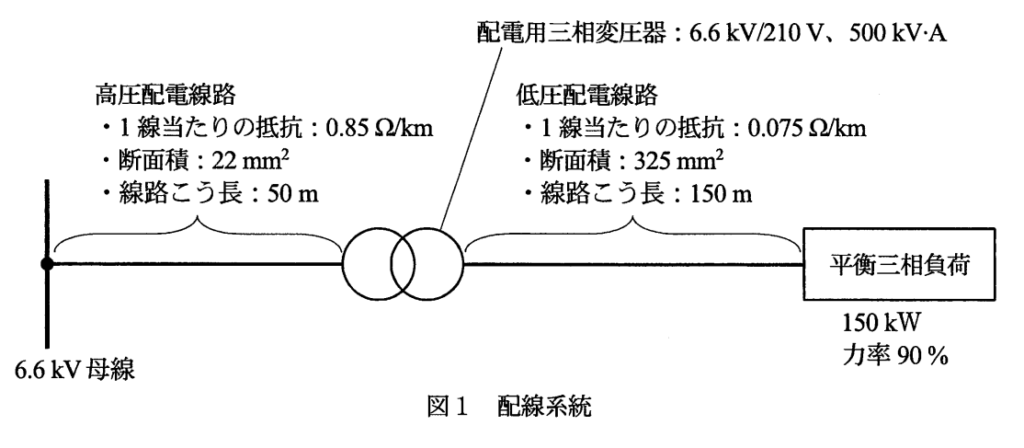
図1で変圧器の1次側電圧と2次側電圧が分かっている。公式を用い、変圧器1次側電流を求める。
\begin{eqnarray}
α=\frac{V_1}{V_2}&=&\frac{I_2}{I_1} \\
\frac{V_1}{V_2}&=& \frac{I_2}{I_1} \\
{I_1}&=& \frac{V_2}{V_1}\times{I_2} \\
&=& \frac{210}{6600}\times{458.2279} \\
&=& {14.5799[A]} \\
\end{eqnarray}
損失電力量を求める
\begin{eqnarray}
P&=& 3I^2r[kw]
\end{eqnarray}
P:3相分の線路損失[kW]、I:線路電流[A]、r:線路抵抗[Ω]
図1より1線当たりの抵抗値[Ω/km]、問題文より配線長[m]が与えられている。
配電線路に流れる変圧器1次側の電流I₁と、変圧器2次側の電流I₂が分かったので、公式に代入して変圧器1次側の電力損失P₁と、変圧器2次側のP₂を求める。
\begin{eqnarray}
P_1&=& 3{I_1^2}{r} \\
&=& 3\times14.5799^2\times(0.85\times0.05) \\
&=& 3\times14.5799^2\times0.0425 \\
&=& 27.103[W] \\
\end{eqnarray}
\begin{eqnarray}
P_2&=& 3{I_2^2}{r} \\
&=& 3\times458.2279^2\times(0.075\times0.150) \\
&=& 3\times458.2279^2\times0.01125 \\
&=& 7086.58[W] \\
\end{eqnarray}
よって変更前の電力損失は以下のようになる。
\begin{eqnarray}
P_1+P_2&=& 27.103+7086.58=7113.683[W] \\
\end{eqnarray}
次に、変更後の各電力損失P₁’とP₂’を求める。
\begin{eqnarray}
P_1’&=& 3{I_1^2}{r’} \\
&=& 3\times14.5799^2\times(0.85\times0.150) \\
&=& 3\times14.5799^2\times0.1275 \\
&=& 81.309[W] \\
\end{eqnarray}
\begin{eqnarray}
P_2’&=& 3{I_2^2}{r’} \\
&=& 3\times458.2279^2\times(0.075\times0.05) \\
&=& 3\times458.2279^2\times0.00375 \\
&=& 2362.194[W] \\
\end{eqnarray}
よって変更前の電力損失は以下のようになる。
\begin{eqnarray}
P_1’+P_2’&=& 81.309+2362.194=2443.503[W] \\
\end{eqnarray}
求めたいのは変更前と変更後の電力損失の差であるから、
\begin{eqnarray}
ΔP&=& (P_1+P_2)-(P_1’+P_2’) \\
&=& 7113.683-2443.503 \\
&=& =4670.18 ≒ 4.7[kW] \\
\end{eqnarray}
よって問Bの答えは4.7[kW]であることが分かる。



コメント