三相誘導電動機の等価回路から諸量を求める問題。1)の問題文には誘導電動機の基礎が説明されているのでこの内容は理解しておきたい。また、本問は公式が問題文に与えられているので問題をよく読めば解くことができる問題がほとんどである。
- 難易度 ★★☆☆☆
- 重要度 ★★★★★



問題と解答群を俯瞰する
1)の問題全体と解答群全体を眺めた時、以下の点に気付きたい。
- ii)の式はよく使う公式であるので、アである。分からなくても、問題文に滑りsのみを用いるとあるから、ア~ウが問12の選択肢となる。
- エとキの式は見たことがない。解答ではない。(気がする、というレベルでいい)
- 問題10は、知らなくても②の式とii)の式から求めることができる。
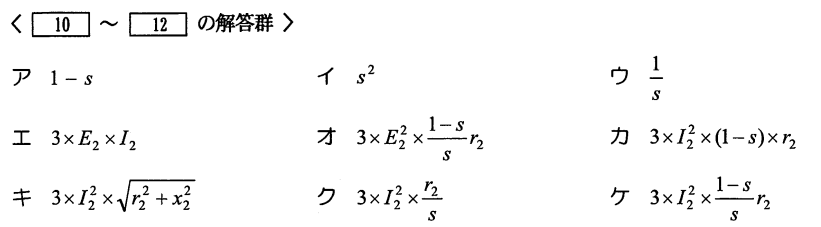
電動機の二次入力の式を求める
\begin{eqnarray}
P_2&=& 3(r_2+R)I_2^2=3\frac{r_2}{s}I_2^2 \\
※R&=& \frac{1-s}{s}\times{r_2} \\
Pc_2&=& 3r_2I_2^2 \\
Po&=& P_2-Pc_2=3\frac{r_2}{s}I_2^2-3r_2I_2^2 \\
&=& 3(\frac{1-s}{s})r_2I_2^2 \\
P_2:Pc_2:Po&=& 1:s:1-s \\
Po’&=& Po-Pm
\end{eqnarray}
P₂:二次入力[W]、Pc₂:二次銅損[W]、Po:機械的出力[W]、Pm:機械損[W]、Po’:軸出力[W]、r₂:1相あたりの二次巻線抵抗[Ω]、I₂:二次電流[A]、s:滑り[%]
i)の問題文から、二次銅損PC₂の式は分かっている。また、ii)の公式からP₂とPC₂の比が分かっている。
この2つの式を用い、式変形を行うと以下のとおりになる。
\begin{eqnarray}
P_2:Pc_2:Po&=& 1:s:1-s \\
P_2:Pc_2&=& 1:s \\
P_2:3I_2^2r_2&=& 1:s \\
sP_2&=& 3I_2^2r_2 \\
P_2&=& \frac{3I_2^2r_2}{s} \\
P_2&=& 3I_2^2\frac{r_2}{s} \\
\end{eqnarray}
よって問10の答えはクであることが分かる。
電動機の機械出力を求める
i)の問題文から、機械出力PoはP₂からPC₂を引いた値であると与えられている。問題文にPC₂の式があり、先ほどP₂の式を求めたので、そのまま計算することができる。
\begin{eqnarray}
Po&=& P_2-Pc_2 \\
&=& 3I_2^2\frac{r_2}{s}-3I_2^2r_2 \\
&=& 3I_2^2\frac{1-s}{s}r_2 \\
\end{eqnarray}
よって問11の答えはケであることが分かる。
二次入力、二次銅損、機械出力の関係式を求める
この公式は誘導電動機では頻出であるので覚えておくこと。しかし、今回は覚えてなくても解くことができる。問題文の与えられた式と先ほど求めた式を用いて解いていく。
\begin{eqnarray}
P_2:Pc_2:Po&=& 1:s:(問12) \\
P_2:Po&=& 1:(問12) \\
(問12)P_2:&=& Po \\
(問12)&=& \frac{Po}{P_2} \\
&=& \frac{3I_2^2\frac{1-s}{s}r_2}{3I_2^2\frac{r_2}{s}} \\
&=& {\frac{1-s}{s}r_2}\times\frac{s}{r_2} \\
&=& 1-s \\
\end{eqnarray}
よって問12の答えはアであることが分かる。
運転時のすべりを求める
問題文に必要な項がすべて与えられているので、公式に代入して求める。
\begin{eqnarray}
Ns&=& \frac{120f}{P} \\
N&=& \frac{120f(1-s)}{P} \\
\end{eqnarray}
Ns:同期速度[min⁻¹]、N:回転速度[min⁻¹]、f:周波数[Hz]、P:極数、s:滑り[%]
\begin{eqnarray}
N&=& \frac{120f(1-s)}{P} \\
(1-s)&=& \frac{NP}{120f} \\
&=& \frac{1455\times4}{120\times50} \\
&=& {0.97} \\
s&=& {1-0.97} \\
&=& {0.03} \\
\end{eqnarray}
よって問Aの答えは3.0[%]であることが分かる。
電動機の軸出力を求める
\begin{eqnarray}
P_2&=& 3(r_2+R)I_2^2=3\frac{r_2}{s}I_2^2 \\
※R&=& \frac{1-s}{s}\times{r_2} \\
Pc_2&=& 3r_2I_2^2 \\
Po&=& P_2-Pc_2=3\frac{r_2}{s}I_2^2-3r_2I_2^2 \\
&=& 3(\frac{1-s}{s})r_2I_2^2 \\
P_2:Pc_2:Po&=& 1:s:1-s \\
Po’&=& Po-Pm
\end{eqnarray}
P₂:二次入力[W]、Pc₂:二次銅損[W]、Po:機械的出力[W]、Pm:機械損[W]、Po’:軸出力[W]、r₂:1相あたりの二次巻線抵抗[Ω]、I₂:二次電流[A]、s:滑り[%]
問題文から、③の式を用いて機械出力Poを求め、機械損を引くことで軸出力が求まると分かっている。必要な項がすべて与えられているので、公式に代入して求めることができる。
まず機械出力を求める。
\begin{eqnarray}
Po&=& 3(\frac{1-s}{s})r_2I_2^2 \\
&=& 3(\frac{1-0.04}{0.04})\times0.21\times20^2 \\
&=& 8148[w] \\
\end{eqnarray}
機械出力Poから機械損Pmを引くことで軸出力Po’が求まるので、
\begin{eqnarray}
Po’&=& Po-Pm=8148-128 \\
&=& 8020[w] \\
\end{eqnarray}
よって問Bの答えは8020[W]であることが分かる。
電動機の一次入力を求める
誘導電動機の一次側とはつまり固定子である。二次入力に一次側で発生する損失(一次銅損と鉄損)を足すことで一次入力を求めることができる。一次側では鉄損が発生するので、忘れないようにすること。
まず二次入力を求める。
\begin{eqnarray}
P_2&=& 3\frac{r_2}{s}I_2^2 \\
&=& 3\frac{0.21}{0.03}\times20^2 \\
&=& 8400[W] \\
\end{eqnarray}
次に、二次銅損を求める。
\begin{eqnarray}
Pc_2&=& 3r_2I_2^2 \\
&=& 3\times0.21\times20^2 \\
&=& 252[W] \\
\end{eqnarray}
問題文より、一次銅損は二次銅損の1.5倍であるので、
\begin{eqnarray}
Pc_1&=& 252\times1.5=378
\end{eqnarray}
鉄損は1相あたり30Wなので、3相分は90Wである。
これらの損失を足し合わせると、
\begin{eqnarray}
P_1&=& P_2+Pc_1+Pi \\
&=& 8400+378+90 \\
&=& 8868[W] \\
\end{eqnarray}
よって問Cの答えは8868[W]であることが分かる。
効率を求める
問題文に式が載っているので、代入する。効率は出力/入力で求まる。
\begin{eqnarray}
η&=&\frac{Po’}{P_1} \\
&=& \frac{8020}{8868} \\
&=& 0.904 ≒ 90.4[%] \\
\end{eqnarray}
よって問Dの答えは90.4[%]であることが分かる。



コメント