配電線路の力率改善時の変化量を求める問題。基礎的な問題の詰め合わせなので確実に解けるようにしておきたい。
- 難易度 ★★☆☆☆
- 重要度 ★★★★★


負荷の合成最大需要電力を求める
問題文に不等率が与えられているので、公式から求めることができる。
ポイント
\begin{eqnarray}
不等率=\frac{各負荷の電力最大需要電力の和[kw]}{合成最大需要電力[kw]}
\end{eqnarray}
※不等率は必ず1以上となる
\begin{eqnarray}
不等率&=& \frac{各負荷の最大需要電力の和[kw]}{合成最大需要電力[kw]} \\
合成最大需要電力[kw]&=& \frac{各負荷の最大需要電力の和[kw]}{不等率} \\
&=& \frac{5500+400+850}{1.2} \\
&=& 1500 \\
\end{eqnarray}
よって問Aの答えは1500[kW]であることが分かる。
全体の無効電力から力率を求める
この手の問題が出たときは、以下のベクトル図を思い浮かべると考えやすい。
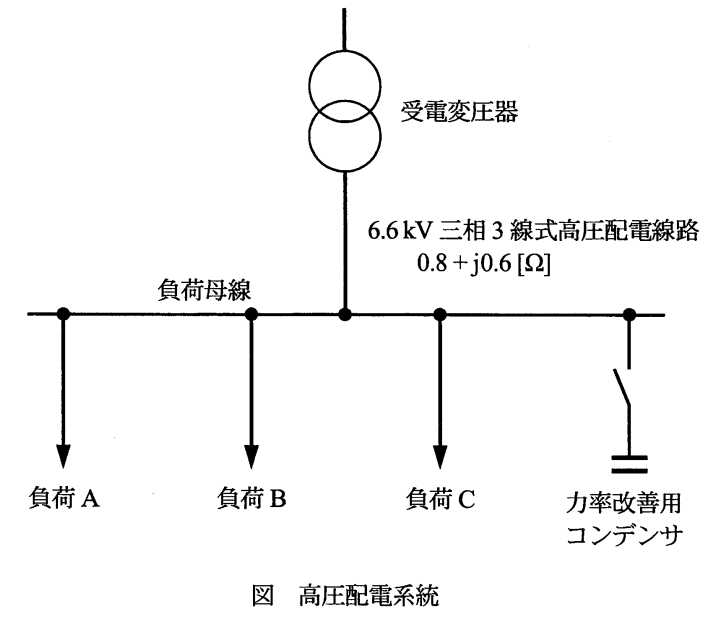
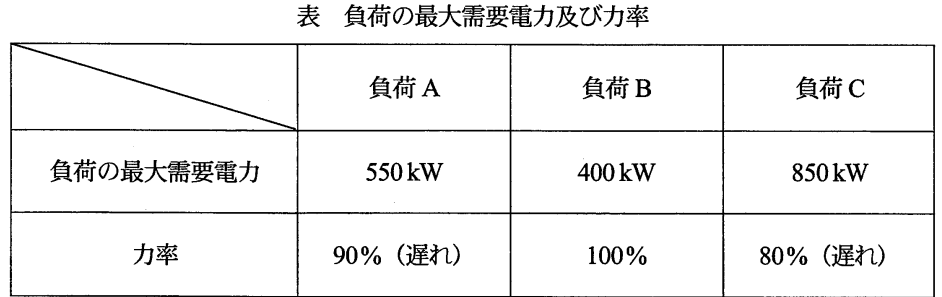
抵抗成分とリアクタンス成分はそれぞれcosθとsinθをかけることで算出できる。
各負荷の無効電力を求めていく。まず、問題文より、負荷Bの有効電力は以下のように求められる。
\begin{eqnarray}
sinθa&=& 1500-550-850
&=& {100[kW]} \\
\end{eqnarray}
問題文に無効率sinθは与えられていないので、負荷Aの無効電力Qaを求めるためにsinθaを求める。
\begin{eqnarray}
sinθa&=& \sqrt{1-cosθa^2} \\
&=&\sqrt{1-0.9^2} \\
&=& {0.4359} \\
\end{eqnarray}
負荷Cも同様に求めることができるが、cosθ=0.8のとき、sinθ=0.6である。これはよく出る組み合わせなので覚えておくとよい。なお、cosθ=0.6のとき、sinθ=0.8である。
よって、sinθb=0.6である。
負荷Bは力率cosθが1なので、sinθは0である。これは覚えておくこと。
無効率sinθが分かったので、無効電力を求めていく。
\begin{eqnarray}
Qa&=& {Sa}\times{sinθa}\\
&=& \frac{Pa}{cosθa}\times{sinθa}\\
&=& \frac{550}{0.9}\times{0.4359}\\
&=& {266.38}[kVar]\\
\end{eqnarray}
\begin{eqnarray}
Qb&=& \frac{Pb}{cosθb}\times{sinθb}\\
&=& \frac{100}{1}\times{0}\\
&=& {0}[kVar]\\
\end{eqnarray}
\begin{eqnarray}
Qc&=& \frac{Pc}{cosθc}\times{sinθc}\\
&=& \frac{850}{0.85}\times{0.6}\\
&=& {637.5}[kVar]\\
\end{eqnarray}
\begin{eqnarray}
Q&=& 266.38+0+637.5 \\
&=& {903.88 ≒ 904}[kVar]\\
\end{eqnarray}
よって問Bの答えは904[kVar]であることが分かる。
総合力率を求める
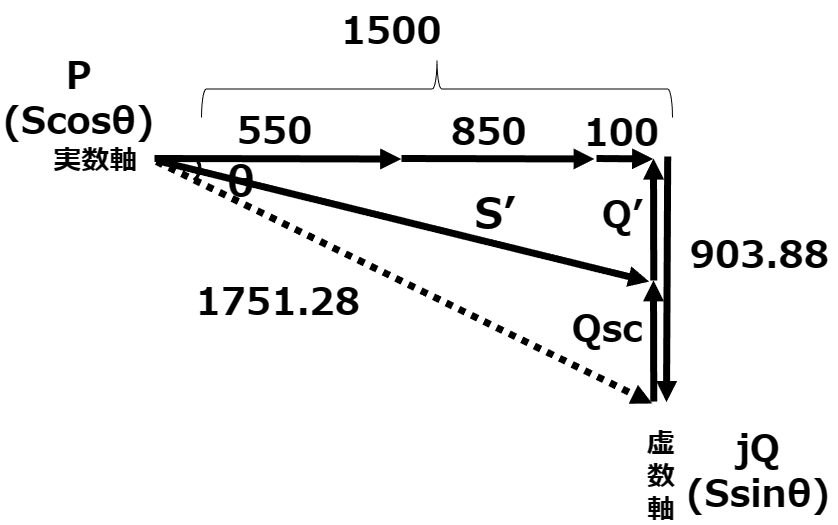
ここまでのベクトル図を整理すると以下のようになる。
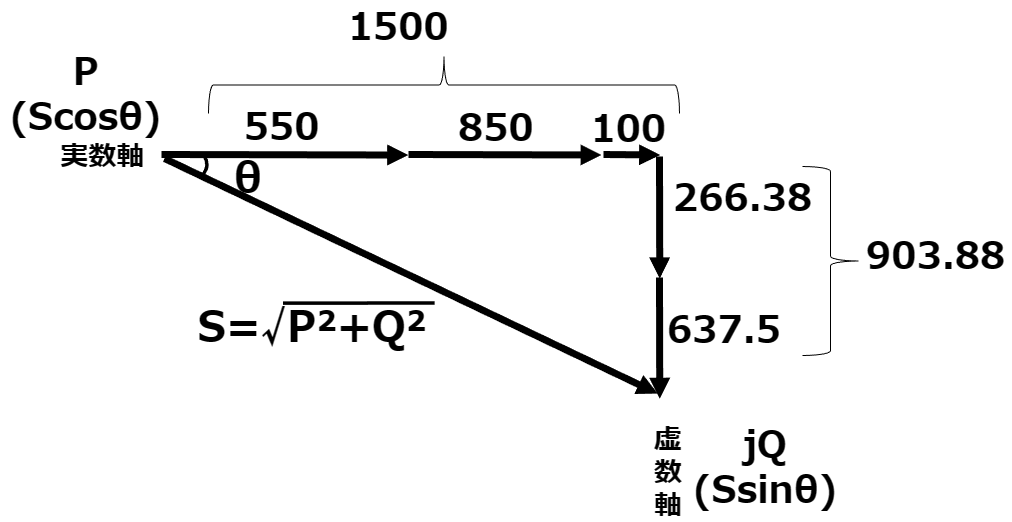
合計ベクトルからSを求め、総合力率を求めていく。
\begin{eqnarray}
S&=& \sqrt{P^2+Q^2} \\
&=& \sqrt{1500^2+903.88^2} \\
&=& 1751.28[kVA] \\
\end{eqnarray}
\begin{eqnarray}
cosθ&=& \frac{P}{S} \\
&=& \frac{1500}{1751.28} \\
&=& {0.8565 ≒ 0.86}\\
\end{eqnarray}
よって問Cの答えは86[%]であることが分かる。
力率改善に必要なコンデンサの容量を求める
3)で総合力率が求まったので、改善後の皮相電力S’を求めれば、以下のベクトル図からQ’を求めることができる。
\begin{eqnarray}
S&=& \frac{P}{cosθ} \\
&=& \frac{1500}{0.95} \\
&=& 1578.95[kVA] \\
\end{eqnarray}
\begin{eqnarray}
S&=& \sqrt{P^2+Q^2} \\
Q&=& \sqrt{S^2-P^2} \\
&=& \sqrt{1578.95^2-1500^2} \\
&=& 493.03[kVar] \\
\end{eqnarray}
2)で求めたコンデンサ投入前の無効電力と、今求まった力率改善後の無効電力の差が投入したコンデンサ容量であるから、
\begin{eqnarray}
Q&=& 903.88-493.03 \\
&=& 410.85 ≒411 [kVar] \\
\end{eqnarray}
よって問Dの答えは411[kVar]であることが分かる。
力率改善後の線路電流を求める
\begin{eqnarray}
P&=& \sqrt{3}IVcosθ \\
\end{eqnarray}
P:有効電力[kW]、I:電流[A]、V:電圧[V]、cosθ:力率
4)は問題文にcosθが与えられているので、公式に代入するだけで求められる。
\begin{eqnarray}
P&=& \sqrt{3}IVcosθ \\
I&=& \frac{P}{\sqrt{3}IVcosθ} \\
&=& \frac{1500}{\sqrt{3}\times6600\times0.95} \\
&=& 138.126 ≒ 138[A] \\
\end{eqnarray}
よって問Eの答えは138[A]であることが分かる。
線路電圧降下から送り出し電圧を求める
\begin{eqnarray}
ΔV&=& \sqrt{3}I(Rcosθ+Xsinθ) \\
\end{eqnarray}
ΔV:電圧降下[V]、I:電流[A]、R:線路抵抗[Ω]、X:線路リアクタンス[Ω]、cosθ:力率、sinθ:無効率
問題文に公式、図に各値が与えられているので、代入して求める。
無効率sinθのみ未知なので、まずsinθを求める。
\begin{eqnarray}
sinθ&=& \sqrt{1-cosθ^2} \\
&=& \sqrt{1-0.95^2} \\
&=& 0.3122 \\
\end{eqnarray}
公式に必要なすべての値がでたので、代入する。
\begin{eqnarray}
ΔV&=& \sqrt{3}I(Rcosθ+Xsinθ) \\
&=& \sqrt{3}\times138.13\times(0.8\times0.95+0.6\times0.312) \\
&=& 226.61[V] \\
\end{eqnarray}
\begin{eqnarray}
V+ΔV&=&{6600}+{226.61}\\
&=& {6826.61} ≒ {6.83[kV]} \\
\end{eqnarray}
よって問Fの答えは6.83[kV]であることが分かる。



コメント