配電線路の力率改善時の変化量を求める問題。よく見る頻出問題のため確実に解けるようにしたい。
- 難易度 ★★★☆☆
- 重要度 ★★★★★

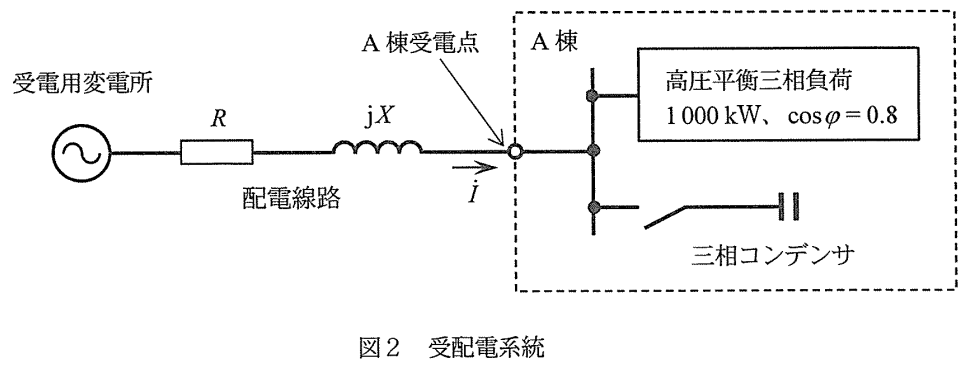

配電線路に流れる電流を求める
\begin{eqnarray}
P&=& \sqrt{3}IVcosθ \\
\end{eqnarray}
P:有効電力[kW]、I:電流[A]、V:電圧[V]、cosθ:力率
問題文に計算に必要な数値がすべてあるので、公式に代入するだけでよい。
\begin{eqnarray}
I&=& \frac{P}{\sqrt3Vcosθ} \\
&=& \frac{1000\times10^3}{\sqrt3\times6600\times0.8} \\
&=& {109.349 ≒ 109[A]} \\
\end{eqnarray}
よって問Aの答えは109[A]であることが分かる。
配電線路の電圧降下を求める
\begin{eqnarray}
ΔV&=& \sqrt{3}I(Rcosθ+Xsinθ) \\
\end{eqnarray}
ΔV:3相分の電圧降下[V]、I:電流[A]、R:回路抵抗[Ω]、X:リアクタンス[Ω]、cosθ:力率、sinθ:無効率
未知数だった電流は1)で判明した。
問題文より、配電線路の1kmあたりの抵抗とリアクタンスの値と、配電線路全長が分かっているので、全体の配線抵抗RとリアクタンスXを求める。
\begin{eqnarray}
R&=& 0.3\times1.5=0.45[Ω] \\
X&=& 0.5\times1.5=0.75[Ω] \\
\end{eqnarray}
計算に必要な数値がでたので、公式に代入しΔVを導いていく。
cosθ=0.8のとき、sinθ=0.6であるので、
\begin{eqnarray}
ΔV&=& \sqrt{3}I(Rcosθ+Xsinθ) \\
&=& \sqrt{3}\times109.35\times(0.45\times0.8+0.75\times0.6) \\
&=& \sqrt{3}\times109.35\times(0.36+0.45) \\
&=& {153.4 ≒ 153[V]} \\
\end{eqnarray}
よって問Bの答えは153[V]であることが分かる。
念のため記載すると、sinθの求め方は以下のとおりである。
\begin{eqnarray}
sinθ&=& \sqrt{1-cosθ^2} \\
&=&\sqrt{1-0.8^2} \\
&=& {0.6} \\
\end{eqnarray}
力率改善に必要なコンデンサ容量を求める
この手の問題が出たときは、以下のベクトル図を思い浮かべると考えやすい。
抵抗成分とリアクタンス成分はそれぞれcosθとsinθをかけることで算出できる。
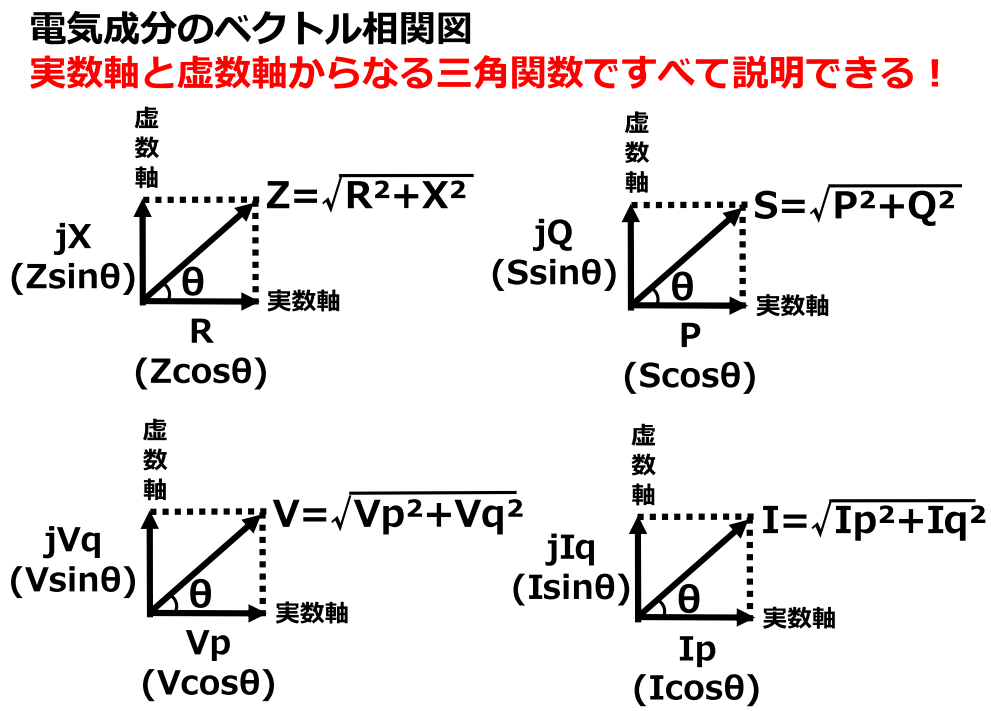
まず、コンデンサを投入すると無効電力が変わるので、無効電力を求める。
\begin{eqnarray}
Q&=& Ssinθ \\
&=& \frac{P}{cosθ}\times{sinθ} \\
&=& \frac{1000}{0.8}\times0.6 \\
&=& 750[kVar] \\
\end{eqnarray}
ここまでをベクトル図で表すと以下のとおりとなる。
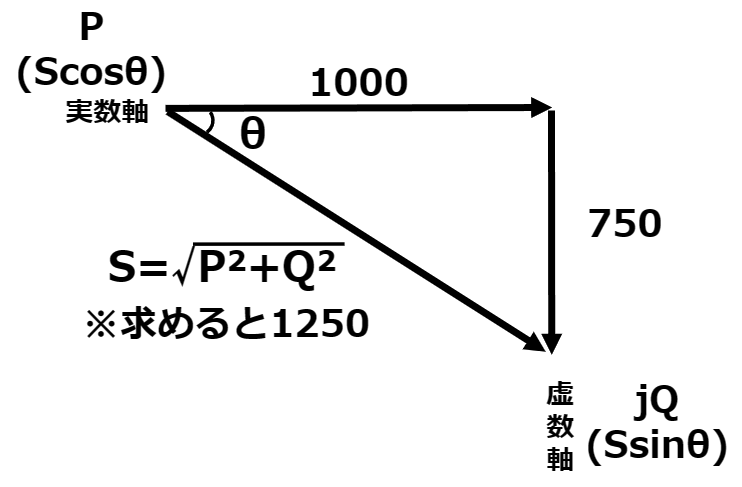
このベクトル図を最終的には以下の形としていき、Qscを求める。
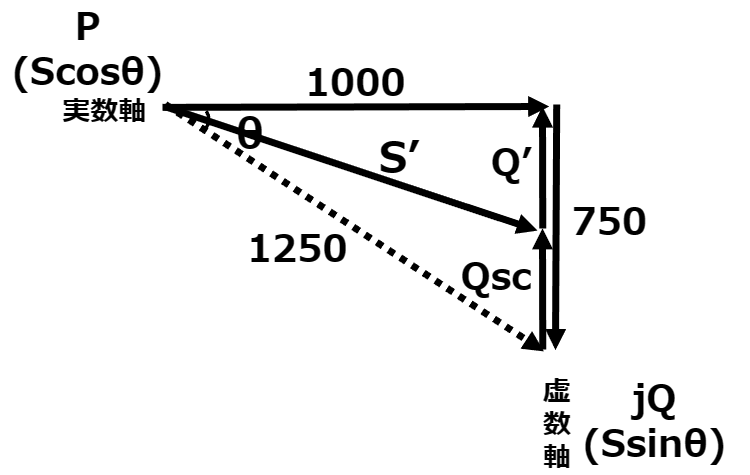
次に、力率が改善後の無効電力Q’を求めていく。
無効電力Q’を求めるため、力率改善後の皮相電力S’を求める。
\begin{eqnarray}
S’&=& \frac{P}{cosθ₂} \\
&=& \frac{1000}{0.95} \\
&=& 1052.631[kVA] \\
\end{eqnarray}
次に、求めた皮相電力S’から、力率改善後の無効電力Q’を求める。
\begin{eqnarray}
Q’&=& \sqrt{S’^2-P^2} \\
&=& \sqrt{1052.631^2-1000^2} \\
&=& 328.68[kVar] \\
\end{eqnarray}
投入したコンデンサの容量Qscは、力率改善前後の無効電力の差であるから、以下のとおりとなる。
\begin{eqnarray}
Qsc&=& 750-421.32 ≒ {421[kVar]} \\
\end{eqnarray}
よって問Cの答えは421[kVar]であることが分かる。
力率改善後の線路損失を求める
\begin{eqnarray}
P&=& 3I^2r[kw]
\end{eqnarray}
P:3相分の線路損失[kW]、I:線路電流[A]、r:線路抵抗[Ω]
1)で求めたIがI₁なので、公式に代入してP₁を求める。
\begin{eqnarray}
P₁&=& 3{I₁^2}{r} \\
&=& 3\times109.349^2\times0.45 \\
&=& 16142.225[W] \\
\end{eqnarray}
I₂は未知だが、1)と同じ要領で求めることができるので、
\begin{eqnarray}
I₂&=& \frac{P}{\sqrt3Vcosθ₂} \\
&=& \frac{1000\times10^3}{\sqrt3\times6600\times0.95} \\
&=& {92.084[A]} \\
\end{eqnarray}
I₂が分かったので、公式に代入してP₂を求める。
\begin{eqnarray}
P₂&=& 3{I₂^2}{r} \\
&=& 3\times92.084^2\times0.45 \\
&=& 11447.275[W] \\
\end{eqnarray}
問われているのはコンデンサ未接続のときの何%になったかなので、未接続の時が分母にくる。
以下のとおりとなる。
\begin{eqnarray}
\frac{P₂}{P₁}&=&\frac{11447.275}{16142.225}\\
&=& {0.70915} ≒ {71[%]} \\
\end{eqnarray}
よって問Dの答えは71[%]であることが分かる。


コメント