日負荷曲線を用いた配電コントロールの問題です。過去問にも類題が多いので確実に解けるようにしましょう。
- 難易度 ★★★☆☆
- 重要度 ★★★★★


1日の無負荷損を求める
問題文より、変圧器の無負荷損は0.3[kW]である。無負荷損は一定であるから、1日の運転時間を掛けて無負荷損を求める。
\begin{eqnarray}
Pi&=& 0.3\times24 \\
&=& 7.2[kwh]\\
\end{eqnarray}
よって問Aの答えは7.2[kWh]であることが分かる。
1日の負荷損を求める
\begin{eqnarray}
Pc&=& {α}^2\times{Pcn}\times{T} \\
&=&(\frac{P}{Pn})^2\times{Pcn}\times{T}\\
\end{eqnarray}
Pc:変圧器の銅損[kw]、α:負荷率、Pcn:全負荷(定格負荷)時の銅損[kw]、
T:運転時間[h]、P:実負荷[kw]、Pn:定格負荷[kw]
※P、PnはそれぞれS、Snでも計算できる。
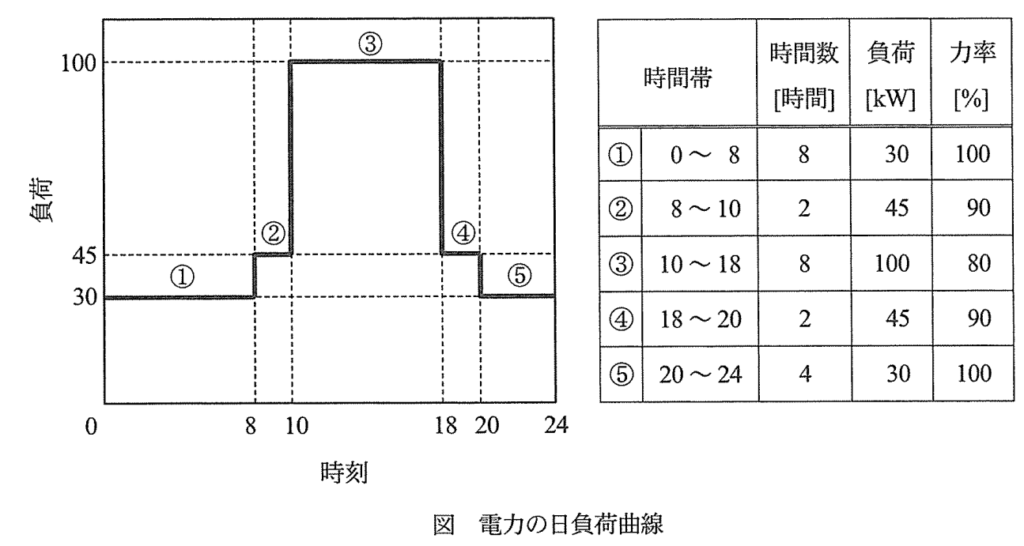
問題文より、変圧器の定格容量は150[kVA]、定格時の変圧器の負荷損は1.5[kW]である。公式より負荷損は負荷率で変化するから、図の日負荷曲線を用い、負荷ごとに運転時間を掛けて無負荷損を求める。
図から30[kW]負荷は12時間、45[kW]負荷は4時間、100[kW]負荷は8時間であることが分かる。
これらの損失電力量を算出し、合計する。
\begin{eqnarray}
Pc30&=& (\frac{30}{{150}\times{1}})^2\times{1.5}\times{12} \\
&=&{0.72[kwh]}\\
\end{eqnarray}
\begin{eqnarray}
Pc45&=& (\frac{45}{{150}\times{0.9}})^2\times{1.5}\times{4} \\
&=&{0.666[kwh]}\\
\end{eqnarray}
\begin{eqnarray}
Pc100&=& (\frac{100}{{150}\times{0.8}})^2\times{1.5}\times{8} \\
&=&{8.333[kwh]}\\
\end{eqnarray}
\begin{eqnarray}
Pc&=& 0.72+0.666+8.333 \\
&=&{9.719 ≒ 9.72[kwh]}\\
\end{eqnarray}
よって問Bの答えは9.72[kWh]であることが分かる。
全日効率を求める
\begin{eqnarray}
η&=& \frac{出力}{入力}=\frac{出力}{出力+損失} \\
&=& \frac{Scosθ}{Scosθ+Pi+Pc} \\
\end{eqnarray}
η:全負荷時効率、S:変圧器定格容量[kVA]、cosθ:力率、Pi:鉄損[kW]、Pc:銅損 [kW]
1日の損失は既に求めているので、出力の合計を求める。
\begin{eqnarray}
P&=& 30\times12+45\times4+100\times8 \\
&=& 1340[kWh] \\
\end{eqnarray}
公式に代入し、全日効率を求める。
\begin{eqnarray}
η&=& \frac{出力}{入力}=\frac{出力}{出力+損失} \\
&=& \frac{Scosθ}{Scosθ+Pi+Pc} \\
&=& \frac{1340}{1340+7.2+9.72} \\
&=& 0.9785 ≒ 98.8[%] \\
\end{eqnarray}
よって問Cの答えは98.8[%]であることが分かる。
力率改善後の損失電力量を求める
時間帯③だけ力率改善するので、改善後のPc100の負荷損を求める。
変わったのは時間帯③のみなので、その差が改善効果である。
\begin{eqnarray}
Pc100’&=& (\frac{30}{{150}\times{0.95}})^2\times{1.5}\times{8} \\
&=&{5.9095 ≒ 5.91[kwh]}\\
\end{eqnarray}
\begin{eqnarray}
Pc&=& 8.333-5.91 \\
&=&{2.423 ≒ 2.42[kwh]}\\
\end{eqnarray}
よって問Dの答えは2.42[kWh]であることが分かる。
負荷率を求める
\begin{eqnarray}
負荷率&=& \frac{平均電力[kw]}{最大電力[kw]} \\
需要率&=& \frac{最大電力[kw]}{設備容量[kw]}\\
\end{eqnarray}
問題文より最大電力100[kW]を配分するので、最大電力が下がる。負荷移動後の最大電力を求める。
そのためにまず、移動する電力量を求める。
\begin{eqnarray}
移動する電力量[kWh]&=& (45-30)\times12 \\
&=& 180[kWh]\\
\end{eqnarray}
この電力量は③の時間(8時間)で消費されるから、1時間あたりに直すと、
\begin{eqnarray}
移動する電力[kW]&=& \frac{180}{8} \\
&=& 22.5[kW]\\
\end{eqnarray}
移動する電力が分かったので、移動前の最大電力100[kW]から移動する電力を引き、移動後の最大電力を求める。
\begin{eqnarray}
移動後の最大電力[kW]&=& 100-22.5 \\
&=& 77.5[kW]\\
\end{eqnarray}
最大電力が分かったため、平均電力 [kW] が分かれば負荷率[%]を求めることができる。以下のとおり平均電力 [kW] を求める。
\begin{eqnarray}
1日の平均電力[kW]&=& \frac{1日の負荷電力の合計[kw]}{24時間} \\
&=& \frac{30\times12+45\times4+100\times8}{24}\\
&=& \frac{360+180+800}{24}\\
&=& {55.83[kW]}\\
\end{eqnarray}
平均電力が分かったので、公式に代入し負荷率を求める。
\begin{eqnarray}
負荷率&=& \frac{平均電力[kw]}{最大電力[kw]} \\
&=& \frac{55.83}{77.5}\\
&=& {0.72038 ≒ 72.0[%]}\\
\end{eqnarray}
よって問Eの答えは72.0[%]であることが分かる。


コメント