三相誘導電動機の等価回路からトルクを求める問題。
- 難易度 ★★★☆☆
- 重要度 ★★★★★
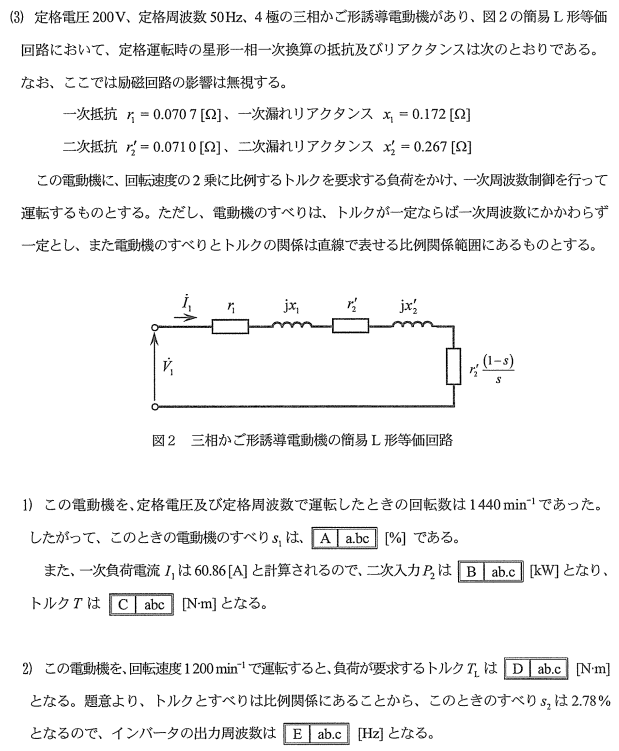
運転時のすべりを求める
問題文に必要な項がすべて与えられているので、公式に代入して求める。
\begin{eqnarray}
Ns&=& \frac{120f}{P} \\
N&=& \frac{120f(1-s)}{P} \\
\end{eqnarray}
Ns:同期速度[min⁻¹]、N:回転速度[min⁻¹]、f:周波数[Hz]、P:極数、s:滑り[%]
\begin{eqnarray}
N&=& \frac{120f(1-s)}{P} \\
(1-s)&=& \frac{NP}{120f} \\
&=& \frac{1440\times4}{120\times50} \\
&=& {0.96} \\
s&=& {1-0.96} \\
&=& {0.04} \\
\end{eqnarray}
よって問Aの答えは4.00[%]であることが分かる。
電動機二次入力を求める
\begin{eqnarray}
P₂&=& 3(r₂+R)I₂^2=3\frac{r₂}{s}I₂^2 \\
※R&=& \frac{1-s}{s}\times{r₂} \\
Pc₂&=& 3r₂I₂^2 \\
Po&=& P₂-Pc₂=3\frac{r₂}{s}I₂^2-3r₂I₂^2 \\
&=& 3(\frac{1-s}{s})r₂I₂^2 \\
P₂:Pc₂:Po&=& 1:s:1-s \\
Po’&=& Po-Pm
\end{eqnarray}
P₂:二次入力[W]、Pc₂:二次銅損[W]、Po:機械的出力[W]、Pm:機械損[W]、
r₂:1相あたりの二次巻線抵抗[Ω]、I₂:二次電流[A]、s:滑り[%]
問題文に必要な項がすべて与えられているので、公式に代入して求めることができる。
\begin{eqnarray}
P₂&=& 3\frac{r₂}{s}I₂^2 \\
&=& 3\frac{0.0710}{0.04}\times60.86^2 \\
&=& 19723.478[w] ≒19.7[kW] \\
\end{eqnarray}
【別解】ちなみにP₂の公式を覚えていなかった場合、以下のように求めることもできる。
\begin{eqnarray}
Po&=& 3(\frac{1-s}{s})r₂I₂^2 \\
&=& 3(\frac{1-0.04}{0.04})0.0710\times60.86^2 \\
&=& 18934.539[w] \\
\end{eqnarray}
\begin{eqnarray}
P₂:Po&=& 1:1-s \\
P₂(1-s)&=& Po \\
P₂&=& \frac{Po}{1-s} \\
&=& \frac{18934.539}{1-0.04} \\
&=& 19723.478[w] ≒19.7[kW] \\
\end{eqnarray}
よって問Bの答えは19.7[kW]であることが分かる。
トルクを求める
\begin{eqnarray}
Po&=& ωT=2π\frac{N}{60}T \\
&=& 2π\frac{(1-s)Ns}{60}T=(1-s)P₂ \\
\end{eqnarray}
Po:機械的出力[W]、ω:回転子の角速度[rad/s]、T:電動機の発生トルク[Nm]、Ns:同期速度[min⁻¹]、s:滑り[%]、P₂:二次入力[W]、
問題文の中で、回転数N=1440が与えられている。また、Poは1)の別解のとおり求められるので、公式に代入する。
\begin{eqnarray}
Po&=& ωT \\
T&=& \frac{Po}{ω} \\
&=& \frac{Po}{2π\frac{N}{60}} \\
&=& \frac{18934}{2π\frac{1440}{60}} \\
&=& 125.627 \\
\end{eqnarray}
よって問Cの答えは126[kW]であることが分かる。
回転数を変えた場合のトルクを求める
問題文より、トルクと滑りは比例関係にあることが分かるので、それぞれの比率で求めることができる。
\begin{eqnarray}
T₁:T₂&=& s₁:s₂ \\
T₂&=& \frac{T₁s₂}{s₁} \\
&=& \frac{125.6\times0.0278}{0.04} \\
&=& 87.3 ≒87.3[Nm] \\
\end{eqnarray}
よって問Dの答えは87.3[Nm]であることが分かる。
※公式解答は87.2[Nm]となっている。有効数字の取り方と思うので、別途確認し修正します。
インバータの出力周波数を求める
問題文から回転数が与えられており、滑りを求めたことから、公式にあてはめ周波数を求めることができる。
\begin{eqnarray}
N&=& \frac{120f(1-s)}{P} \\
f&=& \frac{NP}{120\times(1-s)} \\
&=& \frac{1200\times4}{120\times(1-0.278)} \\
&=& 41.1437 ≒ 41.1[Hz] \\
\end{eqnarray}
よって問Dの答えは41.1[Hz]であることが分かる。



コメント