2回線ループ配電線路のループによる損失の変化と、力率改善時の変化量を求める問題。
電流のベクトル的考え方を身につけるのによい問題。
- 難易度 ★★★★☆
- 重要度 ★★★★☆


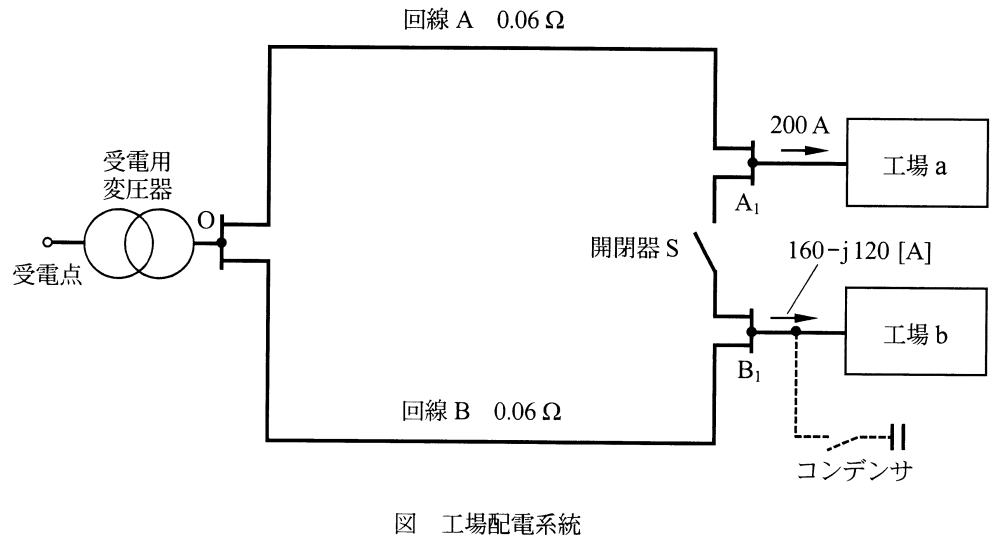
開閉器が開いた状態の線路損失合計を求める
ポイント
\begin{eqnarray}
P&=& 3I^2r[kw]
\end{eqnarray}
P:3相分の線路損失[kW]、I:線路電流[A]、r:線路抵抗[Ω]
回路Aに流れる電流Iaは200[A]、1線あたりの抵抗rは0.06[Ω]である。これらを公式に代入する。
\begin{eqnarray}
PA&=& 3Ia^2r \\
&=& 3\times200^2\times0.06 \\
&=& 7200[W] \\
\end{eqnarray}
回線Bに流れる電流İbは、160-j120[A]である。これは複素数表示となっているので、これから実数と虚数部を合成したIbを求める。
\begin{eqnarray}
Ib&=& \sqrt{Ir^2+Ix^2} \\
&=& \sqrt{160^2+120^2} \\
&=& 200[A] \\
\end{eqnarray}
電流値がでたので、回線Aと同様に公式に代入し、合計する。
\begin{eqnarray}
PB&=& 3Ib^2r \\
&=& 3\times200^2\times0.06 \\
&=& 7200[W] \\
P&=& PA+PB \\
&=& 7200+7200 \\
&=& 14400 ≒ 14.4[kW] \\
\end{eqnarray}
よって問Aの答えは14.4[kW]であることが分かる。
開閉器が閉じた状態の電流を求める
負荷に流れる電流は変わらないので、各回線の電流を合計する。この際、回線Bの電流はリアクタンス成分(虚数部)の影響で位相がずれているから、先ほど求めた実数と合計して400[A]!とすることはできない。
この手の問題が出たときは、以下のベクトル図を思い浮かべると考えやすい。
抵抗成分とリアクタンス成分はそれぞれcosθとsinθをかけることで算出できる。
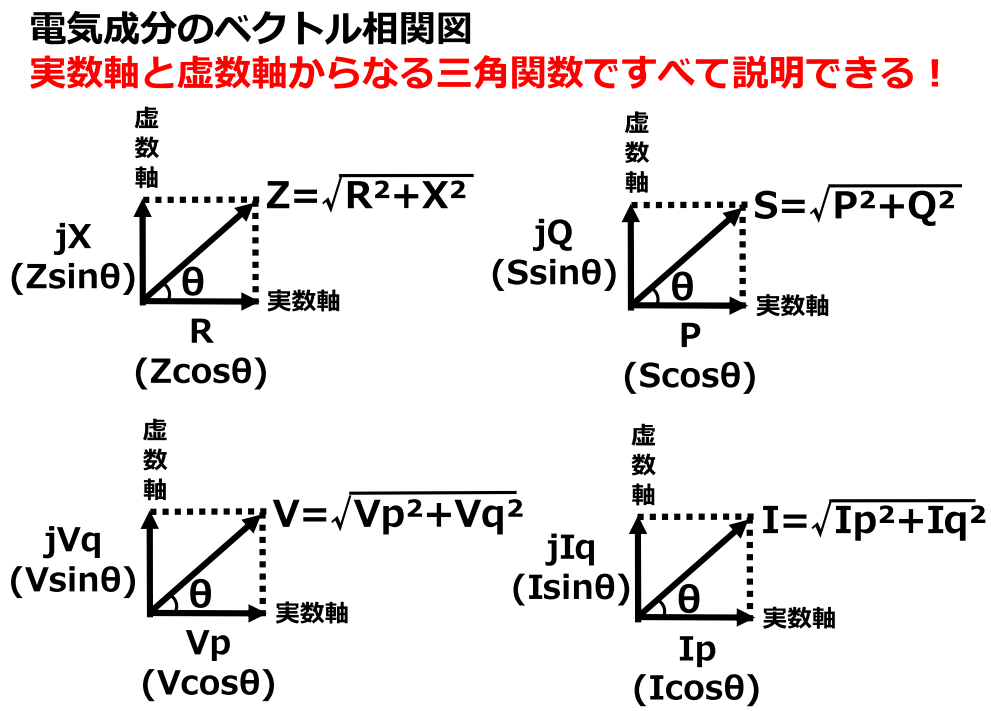
回線Aの200[A]は力率100[%]なので実数、回線Bの160[A]も実数、回線Bの-j120が虚数成分であるから、負荷全体に流れる電流İを以下のとおり合成する。
\begin{eqnarray}
{İ}&=& Ia+Ib \\
&=& 200+160-j120 \\
&=& {360-j120[A]} \\
\end{eqnarray}
この電流が2回線で送られる。かつ、各線路抵抗は同じであるから、各回線に流れる電流İは求めた電流のちょうど半分になるので、
\begin{eqnarray}
{İa’、İb’}&=& \frac{İ}{2} \\
&=& \frac{360-j120}{2} \\
&=& {180-j60[A]} \\
\end{eqnarray}
開閉器Sに流れる電流は、各負荷に必要な電流に対する過不足分である。
今回は工場aは20[A]足りず、-j60[A]が余っている。
一方で、工場bでは20[A]が余り、-j60[A]が足りていない。
よって、開閉器Sに流れる電流İsは20-j60[A]となる。
解答欄は複素数表示で記載するようになっていないので、合成したIを求める。
\begin{eqnarray}
Is&=& \sqrt{Ir^2+Ix^2} \\
&=& \sqrt{20^2+60^2} \\
&=& 63.24 ≒ 63[A] \\
\end{eqnarray}
よって問Bの答えは63[A]であることが分かる。
開閉器が閉じた状態の線路損失を求める
開閉器が閉じた後の各回線の電流値が、ともに180-j60[A]と分かった。
線路損失の公式に代入するため、実数部と虚数部を合成する。
\begin{eqnarray}
{Ia’、Ib’}&=& \sqrt{Ir^2+Ix^2} \\
&=& \sqrt{180^2+60^2} \\
&=& 189.736[A] \\
\end{eqnarray}
公式にあてはめ、改善後の線路損失を求める。今回、回線ABともに電流と抵抗が同じであるから、片方
を求めて2倍すればよい。
\begin{eqnarray}
P’&=& 2\times3I^2r \\
&=& 2\times3\times189.736^2\times0.06 \\
&=& 12959.909[W] \\
P-P’&=& 14400-12959.909 \\
&=& 1440.091 ≒ 1.44[kW] \\
\end{eqnarray}
よって問Cの答えは1.44[kW]であることが分かる。
開閉器が閉じた状態の線路損失を力率改善で再現した際の電流を求める
問題文から、回線Bにコンデンサを投入するので、回線Bの線路損失が改善することが分かる。
逆をいえば、回線Aはそのままなので、回線Bの改善後の線路損失は以下のとおり求まる。
\begin{eqnarray}
PB’&=& P’-PA \\
&=& 12959.901-7200 \\
&=& 5759.901[W] \\
\end{eqnarray}
次に、改善後の電流Ib’’を求める。
\begin{eqnarray}
PB’&=& 3Ib’’^2r \\
Ib’’&=& \sqrt{\frac{PB’}{3r}} \\
&=& \sqrt{\frac{5759.901}{3\times0.06}} \\
&=& 178.884[A] \\
\end{eqnarray}
コンデンサを投入しているのみなので、変化するのは電流のリアクタンス成分(虚数部)のみである。よって、投入後の虚数部を求める。
\begin{eqnarray}
Ib’’&=& \sqrt{Ir^2+Ix’^2} \\
Ix’&=& \sqrt{Ib’’^2-Ir^2} \\
&=& \sqrt{178.884^2-160^2} \\
&=& 79.9967[A] \\
\end{eqnarray}
問題文より、回線Bに流れる電流を進み力率にしてはいけないので、虚数部の変化分はすべて進相コンデンサ側に流れることがわかる。
\begin{eqnarray}
Isc&=& Ix’-Ix \\
&=& 120-79.9967 \\
&=& 40.0033 ≒ 40[A] \\
\end{eqnarray}
よって問Dの答えは40[A]であることが分かる。


コメント