力率改善時の配電線路の損失変化量を求める問題。
電流のベクトル的考え方を身につけるのによい問題。
- 難易度 ★★★☆☆
- 重要度 ★★★★★


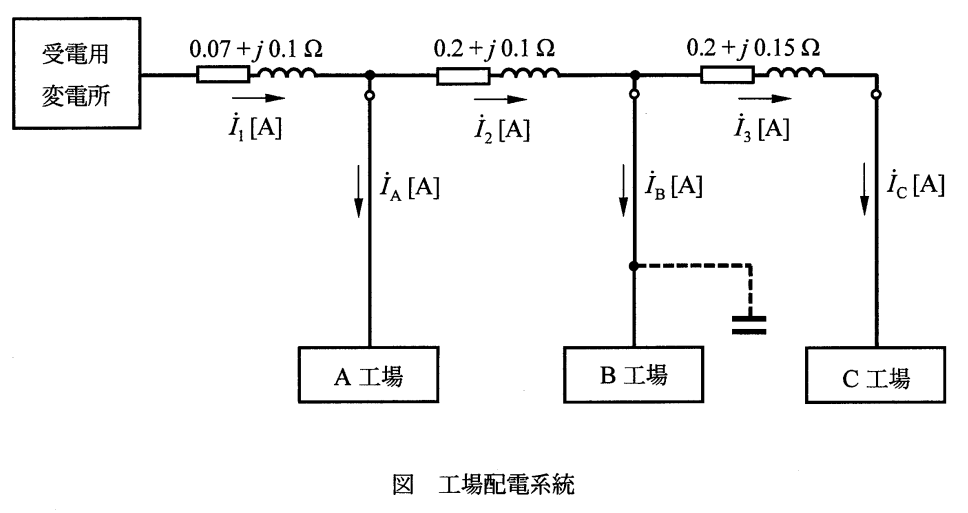
A工場までの分岐点までに流れる電流を求める
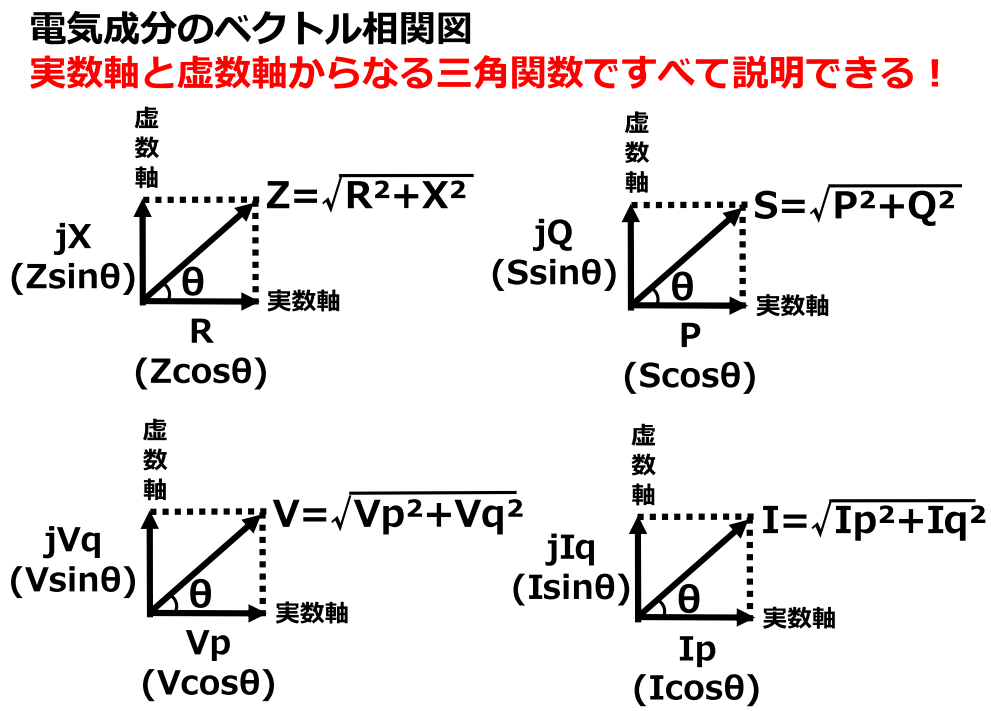
抵抗成分とリアクタンス成分はそれぞれcosθとsinθをかけることで算出できる。
問題文より、各電流値が分かる。電流の関係を図に書き込むと以下のようになる。
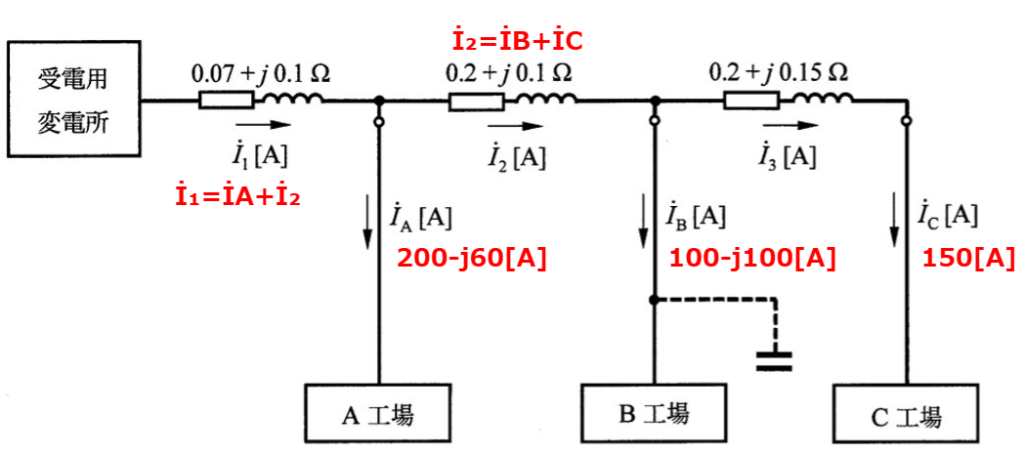
求めたいのはİ₁なので、各電流値の関係から導いていく。İ₃はその後で分岐していないので、İcと同じである。
\begin{eqnarray}
İ_1&=& İ_A+İ_2 \\
&=& İ_A+İ_B+İ_C \\
&=& (200-j60)+(100-j100)+150 \\
&=& 450-j160[A] \\
\end{eqnarray}
問Aは3桁の値で聞かれているから、実数表記である。よって、複素数表記İ₁を実数表記I₁に直すと、
\begin{eqnarray}
I_1&=& \sqrt{İp_1^2+İq_2^2} \\
&=& \sqrt{450^2+160^2} \\
&=& \sqrt{202500+25600} \\
&=& 477.598 ≒ 478[A] \\
\end{eqnarray}
よって問Aの答えは478[A]であることが分かる。
受電用変電所からC工場までの線路損失を求める
ポイント
\begin{eqnarray}
P&=& 3I^2r[kw]
\end{eqnarray}
P:3相分の線路損失[kW]、I:線路電流[A]、r:線路抵抗[Ω]
問題文より、問われているのは以下の図の着色部で発生する線路損失である。
問題文から読み取れなくても、線路損失は抵抗で発生するので、抵抗値の記載がないA工場とB工場への電流は関係ないと分かる。
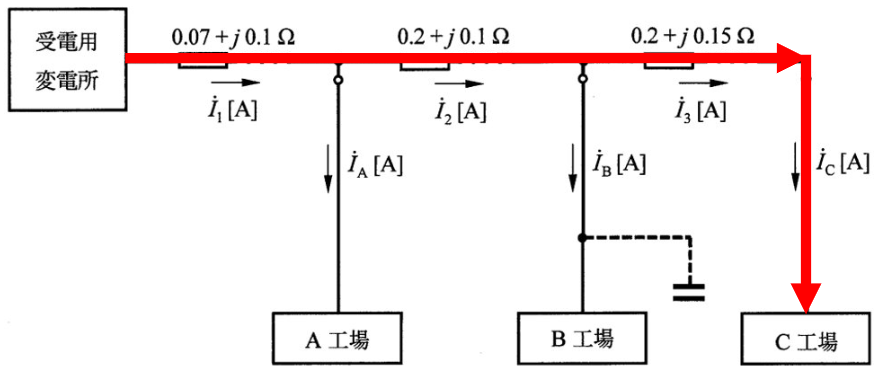
公式を用いるため、I₁、I₂、I₃を求める必要がある。I₁は先ほど求めており、İ₃はその後で分岐していないので、İcと同じである。よって、İ₂を求める。
\begin{eqnarray}
İ_2&=& İ_B+İ_C \\
&=& (100-j100)+150 \\
&=& 250-j100[A] \\
\end{eqnarray}
問Bの使用する公式の電流Iは実数である。よって、複素数表記İ₂を実数表記I₂に直すと、
\begin{eqnarray}
I_2&=& \sqrt{İp_2^2+İq_2^2} \\
&=& \sqrt{250^2+100^2} \\
&=& \sqrt{62500+10000} \\
&=& 269.258[A] \\
\end{eqnarray}
また、İ₃(İc)は虚数部jを持っていないので実数I₃(Ic)と同じ扱いである。
これで回路に流れる電流が全て分かった。図に各線路の抵抗値rが与えられているので、これらを公式に代入する。
\begin{eqnarray}
P_1&=& 3I_1^2r \\
&=& 3\times477.598^2\times0.07 \\
&=& 47900.968[W] \\
\end{eqnarray}
\begin{eqnarray}
P_2&=& 3I_2^2r \\
&=& 3\times269.258^2\times0.2 \\
&=& 43499.922[W] \\
\end{eqnarray}
\begin{eqnarray}
P_3&=& 3I_3^2r \\
&=& 3\times150^2\times0.07 \\
&=& 13500[W] \\
\end{eqnarray}
\begin{eqnarray}
P&=& P_1+P_2+P_3 \\
&=& 47900.968+43499.922+13500 \\
&=& 104899 ≒105 [kW] \\
\end{eqnarray}
よって問Bの答えは105[kW]であることが分かる。
力率改善後の線路損失
問題文から、B工場の電流に進み無効電流が加わると記載があるので、İBは以下になる。
\begin{eqnarray}
İ_B’&=& İ_B+İsc \\
&=& (100-j100)+(j100) \\
&=& 100[A] \\
\end{eqnarray}
また、これによりİ₂も変わるので、
\begin{eqnarray}
İ_2’&=& İ_B’+İ_C \\
&=& 100+150 \\
&=& 250[A] \\
\end{eqnarray}
これにより、İ₁も変わるので、
\begin{eqnarray}
İ_1’&=& İ_A+İ_2′ \\
&=& (200-j60)+100+150 \\
&=& 450-j60[A] \\
\end{eqnarray}
公式は実数で求めるので、複素数İ₁を実数I₁に直すと、
\begin{eqnarray}
I_1&=& \sqrt{İp_1^2+İq_2^2} \\
&=& \sqrt{450^2+60^2} \\
&=& \sqrt{202500+3600} \\
&=& 453.982[A] \\
\end{eqnarray}
これで力率改善後に回路に流れる電流が全て分かった。これらを公式に代入する。
ちなみに、I₃は変化しないので、改善前の線路損失をそのまま使用してよい。
\begin{eqnarray}
P_1’&=& 3I_1’^2r \\
&=& 3\times453.982^2\times0.07 \\
&=& 43280.927[W] \\
\end{eqnarray}
\begin{eqnarray}
P_2’&=& 3I_2’^2r \\
&=& 3\times250^2\times0.2 \\
&=& 37500[W] \\
\end{eqnarray}
\begin{eqnarray}
P_3’&=& 13500[W] \\
\end{eqnarray}
\begin{eqnarray}
P&=& P_1+P_2+P_3 \\
&=& 43280.927+37500+13500 \\
&=& 94280.927[W] \\
\end{eqnarray}
問われているのはコンデンサ接続前を基準として、どれだけの割合になったかなので、
\begin{eqnarray}
P&=& \frac{P’}{P} \\
&=& \frac{94280.927}{104899} \\
&=& 0.89877 ≒ 90[%] \\
\end{eqnarray}
よって問Cの答えは90[%]であることが分かる。


コメント