並列に接続した変圧器2台の負荷分担と日負荷曲線から、最適運転方法を求める問題。
- 難易度 ★★★★☆
- 重要度 ★★★★★

変圧器の負荷分担を求める
変圧器A、B2台を並列運転しているときの負荷分担は、各変圧器の短絡インピーダンス%Zに反比例する。
\begin{eqnarray}
{%ZB’}&=& \frac{SA}{SB} \times{%ZB} \\
SA’&=& \frac{%ZB’}{%ZA+%ZB’}\times{S(※Pでも同じ)} \\
SB’&=& \frac{%ZA}{%ZA+%ZB’}\times{S(※Pでも同じ)} \\
\end{eqnarray}
%ZB’:変圧器Aを基準とした際の、変圧器Bの換算パーセントインピーダンス[%]、
%ZB:変圧器Bのパーセントインピーダンス[%]、
SA:変圧器Aの定格容量[kVA]、SB:変圧器Bの定格容量[kVA]、SA’:変圧器Aの負荷分担容量[kVA]、SB’:変圧器Bの負荷分担容量[kVA]、S:負荷容量[kVA]、P:負荷容量[kW]、
%ZA:変圧器Aのパーセントインピーダンス[%]
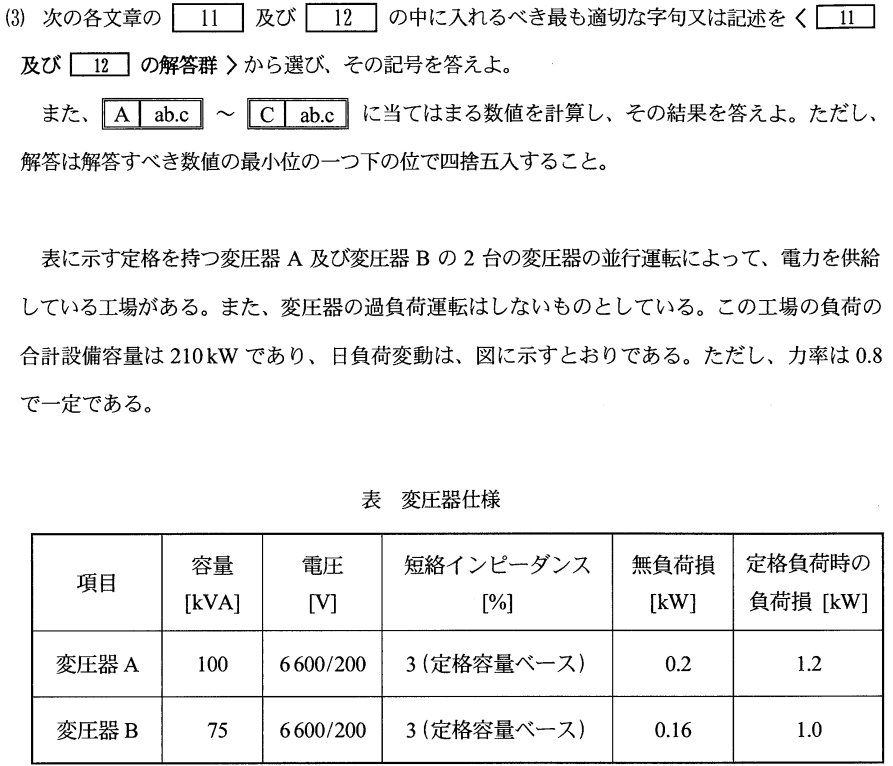
本問題では変圧器Aを基準で解くこととする。まず、基準容量100kVAとした場合の変圧器Bのパーセントインピーダンス%ZB’を求める。表より、各定格容量ベースの短絡インピーダンスが分かっているので、公式に代入して求める。
\begin{eqnarray}
{%ZB’}&=& \frac{SA}{SB} \times{%ZB} \\
&=& \frac{100}{75} \times{3} \\
&=&{4[%]} \\
\end{eqnarray}
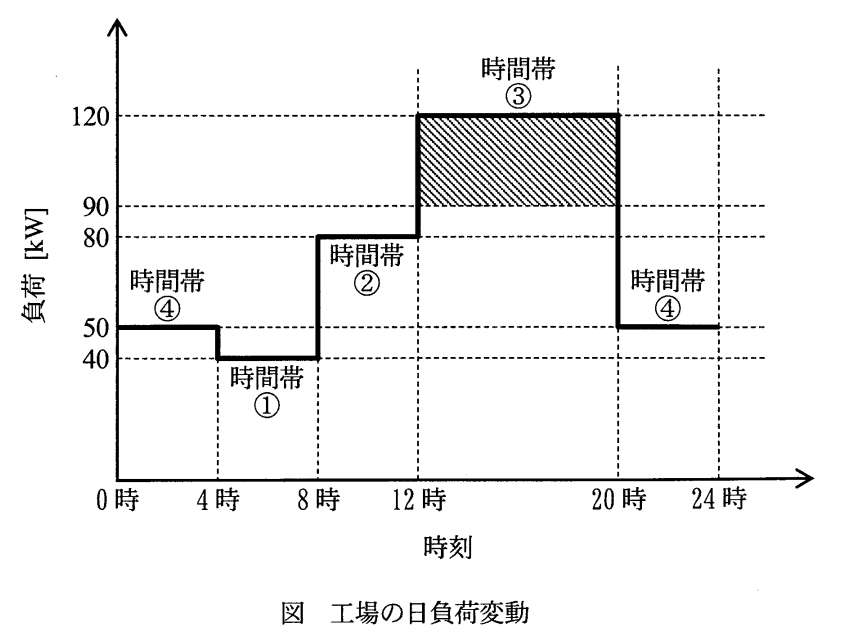
図より時間帯③の負荷は120[kW]なので、それらを公式に代入し、変圧器Aの負荷分担を求める。
\begin{eqnarray}
SA’&=& \frac{%ZB’}{%ZA+%ZB’}\times{S(※Pでも同じ)}\\
&=& \frac{4}{3+4}\times{120} \\
&=& 68.6[kW] \\
\end{eqnarray}
よって問Aの答えは68.6[kW]であることが分かる。
変圧器単独運転の全損失電力量を求める
変圧器の全損失とは無負荷損(鉄損)と負荷損(銅損)の合計のことである。問題より、時間帯②の時、変圧器Aに発生する鉄損と銅損を求めればよい。
まず、鉄損はどの時間においても一定である。表より、0.2[kW]であり、図より②は4時間であるから、
\begin{eqnarray}
Pia&=& 0.2\times4 \\
&=& {0.8[kWh]} \\
\end{eqnarray}
次に、銅損を求める。
定格負荷のα倍の負荷時の負荷損(銅損)の公式
\begin{eqnarray}
Pcα&=& α^2Pc \\
&=& (\frac{Pm}{Pt})^2Pc \\
&=& (\frac{Sm}{St})^2Pc \\
\end{eqnarray}
Pcα:定格負荷のα倍の負荷時の負荷損(銅損)[kW]、α:負荷率、Pc:定格時負荷の負荷損(銅損)[kW]、Pm:負荷の容量[kW]、Pt:変圧器の容量[kW]、Sm:負荷の容量[kVA]、St:変圧器の容量[kVA]
変圧器Aの負荷率が不明であるため、負荷率を求めるために使用時の負荷をだす。
\begin{eqnarray}
P&=& Scosθ \\
S&=& \frac{P}{cosθ} \\
&=& \frac{80}{0.8} \\
&=& {100[kVA]} \\
\end{eqnarray}
使用時の負荷が分かったので、公式に代入して銅損を求める。表より、定格負荷時1.2[kW]であり、図より②は4時間であるから、
\begin{eqnarray}
Pcα&=& α^2Pc \\
&=& (\frac{100}{100})^2\times{1.2}\times4 \\
&=& {4.8[kWh]} \\
Pc+Pi&=& 0.8+4.8 \\
&=& {5.6[kWh]} \\
\end{eqnarray}
よって問Bの答えは5.60[kWh]であることが分かる。
需要率を求める
問題文より合計設備容量、図より最大電力が分かるので公式に代入する。
ポイント
\begin{eqnarray}
負荷率&=& \frac{平均電力[kw]}{最大電力[kw]} \\
需要率&=& \frac{最大電力[kw]}{設備容量[kw]}\\
\end{eqnarray}
\begin{eqnarray}
需要率&=& \frac{最大電力[kw]}{設備容量[kw]} \\
&=& \frac{120}{210} \\
&=& 0.5714 \\
\end{eqnarray}
よって問Bの答えは57.1[%]であることが分かる。
需要率を下げるための方法を考える
需要率は以下の公式から求まる。
ポイント
\begin{eqnarray}
需要率&=& \frac{最大電力[kw]}{設備容量[kw]}\\
\end{eqnarray}
負荷の合成設備容量は変割らないから、最大電力を下げればよい。
解答群の中で、一番最大電力を小さくできるパターンを考える。
問題文より、30[kW]×8時間の240[kWh]を移動させる。
まず、時間帯①は4時間であるから、
\begin{eqnarray}
増加する負荷&=& \frac{240}{4}\\
&=& 60[kW] \\
\end{eqnarray}
\begin{eqnarray}
最大電力①&=& 40+60\\
&=& 100[kW] \\
\end{eqnarray}
次に、時間帯②は①と同じ4時間であり、すでに①より負荷が大きいので①より小さくならないので棄却できる。
次に、時間帯④を考えると、
\begin{eqnarray}
増加する負荷&=& \frac{240}{8}\\
&=& 30[kW] \\
\end{eqnarray}
\begin{eqnarray}
最大電力④&=& 50+30\\
&=& 90[kW] \\
\end{eqnarray}
よって、最大電力は④<①<②になるので、問11の答えはウであることが分かる。
最大負荷時に動かす必要のある変圧器を考える
時間帯③から④に負荷を移動した際、最大負荷が90[kW]になる。
このときの負荷が、変圧器容量で足りているのかを考えればよい。
問題文より、力率cosθは一定であるから、以下のとおり最大負荷を求めることができる。
\begin{eqnarray}
P&=& Scosθ \\
S&=& \frac{P}{cosθ} \\
&=& \frac{90}{0.8} \\
&=& {112.5[kVA]} \\
\end{eqnarray}
最大負荷は変圧器Aの定格容量100[kVA]より大きく、変圧器Aのみでは対応できない。
よって、変圧器A、B両方動かす必要があるので、問12の答えはオであることが分かる。



コメント